tìm tất cả các sô tự nhiên n sao cho : 7^n+147 là số chình phương.Ai giúp mình bài này với.tks nhiều

Những câu hỏi liên quan
Tìm tất cả các số tự nhiên n sao cho 7n + 147 là số chính phương.
Vì \(7^n+147\) là số chính phương
=> Đặt: \(7^n+147\) với a là số nguyên khi đó ta có:
\(7^n+147=a^2\)không mất tính tổng quát g/s a nguyên dương
mà: n là số tự nhiên nên \(7^n⋮7\); \(147=7^2.3⋮7\)=> \(a^2⋮7\)=> \(a⋮7\)=> \(a^2⋮7^2\)
=> \(7^n⋮7^2\)=> n \(\ge\)2
+) Với n = 2k khi đó: \(k\ge1\)
Ta có: \(7^{2k}+147=a^2\)
<=> \(\left(a-7^k\right)\left(a+7^k\right)=147\)
Vì: \(\hept{\begin{cases}0< a-7^k< a+7^k\\a-7^k;a+7^k⋮7\end{cases}}\)
Do đó: \(\hept{\begin{cases}a+7^k=21\\a-7^k=7\end{cases}}\Leftrightarrow7^k=7\Leftrightarrow k=1\)=> n = 2
Thử lại thỏa mãn
+) Với n = 2k + 1 ta có:
\(7^{2k+1}:4\) dư -1
\(147\): 4 dư 3
=> \(7^{2k+1}+147\) chia 4 dư 2
mà số chính phương chia 4 bằng 0 hoặc 1
=> Loại
Vậy: n = 2
Tìm tất cả các số tự nhiên n sao cho n+1, n+3, n+7, n+9, n+13 và n+15 đêu flaf số nguyên tố.
Làm nhanh giúp mình nhé, mình tick cho
Câu hỏi của Nguyễn Lịch Tiểu - Toán lớp 6 - Học toán với OnlineMath
Em tham khảo tại link trên nhé.
Đúng 0
Bình luận (0)
Mọi người giúp em 4 bài này với mọi người giải bằng tiếng việt hay là tiếng anh cũng dc ạ (tiếng anh thì tốt ạ)bài 1:Gọi n là số tự nhiên sao cho n + 1 và 2n + 1 đều là số chính phương . Chứng minh rằng n chia hết cho 24.bài2:Tìm tất cả các số tự nhiên n sao cho 2n + 1,3n + 1 đều là bình phương hoàn hảo và 6n + 5 là số nguyên tố.bài3:tìm các số nguyên a, b, c sao cho a^4 + b^4 7c^4 +5.bài4:Tìm tất cả các số nguyên dương x, y và các số nguyên tố p sao cho x^2 −3xy + p^2y^2 12p.
Đọc tiếp
Mọi người giúp em 4 bài này với mọi người giải bằng tiếng việt hay là tiếng anh cũng dc ạ (tiếng anh thì tốt ạ)
bài 1:Gọi n là số tự nhiên sao cho n + 1 và 2n + 1 đều là số chính phương . Chứng minh rằng n chia hết cho 24.
bài2:Tìm tất cả các số tự nhiên n sao cho 2n + 1,3n + 1 đều là bình phương hoàn hảo và 6n + 5 là số nguyên tố.
bài3:tìm các số nguyên a, b, c sao cho a^4 + b^4 = 7c^4 +5.
bài4:Tìm tất cả các số nguyên dương x, y và các số nguyên tố p sao cho x^2 −3xy + p^2y^2 = 12p.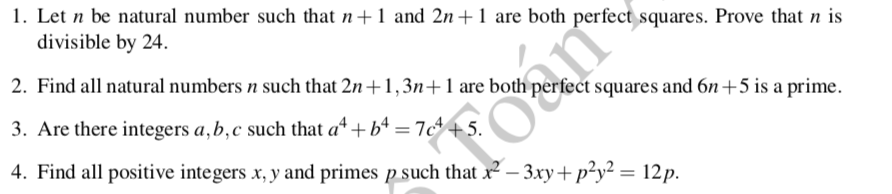
1.
\(2n+1\) luôn lẻ \(\Rightarrow2n+1=\left(2a+1\right)^2=4a^2+4a+1\Rightarrow n=2a\left(a+1\right)\)
\(\Rightarrow n\) chẵn \(\Rightarrow n+1\) lẻ \(\Rightarrow\) là số chính phương lẻ
\(\Rightarrow n+1=\left(2b+1\right)^2=4b^2+4b+1\)
\(\Rightarrow n=4b\left(b+1\right)\)
Mà \(b\left(b+1\right)\) là tích 2 số tự nhiên liên tiếp \(\Rightarrow\) luôn chẵn
\(\Rightarrow4b\left(b+1\right)⋮8\Rightarrow n⋮8\)
Mặt khác số chính phương chia 3 chỉ có các số dư 0 và 1
Mà \(\left(n+1\right)+\left(2n+1\right)=3n+2\) chia 3 dư 2
\(\Rightarrow n+1\) và \(2n+1\) đều chia 3 dư 1
\(\Rightarrow n⋮3\)
\(\Rightarrow n⋮24\) do 3 và 8 nguyên tố cùng nhau
Đúng 2
Bình luận (0)
2.
Lý luận tương tự bài 1, ta được n chẵn
Mặt khác các số chính phương chia 5 chỉ có các số dư 0, 1, 4
Mà: \(\left(2n+1\right)+\left(3n+1\right)=5n+2\) chia 5 dư 2
\(\Rightarrow2n+1\) và \(3n+1\) đều chia 5 dư 1
\(\Rightarrow2n⋮5\Rightarrow n⋮5\) (do 2 và 5 nguyên tố cùng nhau)
\(\Rightarrow n=5k\Rightarrow6n+5=5\left(6k+1\right)\)
- TH1: \(k=0\Rightarrow n=0\Rightarrow6n+5\) là SNT (thỏa mãn)
- TH2: \(k>0\Rightarrow6k+1>0\Rightarrow6n+5\) có 2 ước dương lớn hơn 1 \(\Rightarrow\) không là SNT (loại)
Vậy \(n=0\) là giá trị duy nhất thỏa mãn yêu cầu
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
bài 1 tìm số tự nhiên x nhỏ nhất sao cho x chia cho 5 dư 3 ; x chia cho 7 dư 4
bài 2 cho n là số tự nhiên tìm ƯCLN và BCNN của n và n+2
giúp mình nhé xin các bạn đó sáng mai mình phải nộp bài rồi nếu ai nhanh mình cho 3 tk cảm ơn các bạn nhiều
bài 1 tìm số tự nhiên x nhỏ nhất sao cho x chia cho 5 dư 3 ; x chia cho 7 dư 4
bài 2 cho n là số tự nhiên tìm ƯCLN và BCNN của n và n+2
giúp mình nhé xin các bạn đó sáng mai mình phải nộp bài rồi nếu ai nhanh mình cho 3 tk cảm ơn các bạn nhiều
bai2
UCLN (n,n+2)=d
=>(n+2)-n chia hết cho d
2 chia het cho d
vay d thuoc uoc cua 2={1,2}
nếu n chia hết cho 2 uoc chung lon nhta (n,n+2) la 2
neu n ko chia het cho 2=> (n,n+2) nguyen to cung nhau
BCNN =n.(n+2) neu n le
BCNN=n.(n+2)/2
Đúng 0
Bình luận (0)
Câu 37. Tìm tất cả các số tự nhiên n sao cho (3n + 6 ) là bội của (n – 1.)
giải cho mik bài này siêu gấp ạ
mik củm ưn nhìu
Lời giải:
$3n+6\vdots n-1$
$\Rightarrow 3(n-1)+9\vdots n-1$
$\Rightarrow 9\vdots n-1$
$\Rightarrow n-1\in\left\{\pm 1; \pm 3; \pm 9\right\}$
$\Rightarrow n\in\left\{0; 2; -2; 4; 10; -8\right\}$
Vì $n$ là stn nên $n\in\left\{0; 2; 4; 10\right\}$
Đúng 1
Bình luận (0)
Các bạn giúp mình giải bài này với ạ.Tím tất cả số tự nhiên n thỏa mãn 5n+16 chia hết cho n+2
ta có:5n + 14 chia hết cho n + 2
=>5(n + 2)+4 chia hết cho n + 2
=>4 chia hết cho n + 2
=>n+2 thuộc ước của 4={1;-1;2;-2;4;-4}
=>n ={-1;-3;0;-4;2;-6}
BL
Ta có 5n+16=5n+10+6
Vì 5n+16\(⋮\)n+2
=>5n+10+6\(⋮\)n+2
=>6\(⋮\)n+2 Vì 5n+10 \(⋮\) n+2
=>\(n+2\inƯ\left(6\right)\)
mà Ư(6)={-1;1;-2;2;-3;3;-6;6}
Ta có bảng
| n+2 | -1 | 1 | -2 | 2 | -3 | 3 | -6 | 6 |
| n | -3 | -1 | -4 | 0 | -5 | 1 | -8 | 4 |
vậy .........
Tìm tất cả các các số tự nhiên n để
3^n+6 là số nguyên tố
Các bạn giúp mình với mình cảm ơn rất nhiều
Tìm số tự nhiên n sao cho khi chia các số chính phương cho n thì số dư là tất cả các số chính phương nhỏ hơn n.
Please giúp mình đi!!!!!! Mai mình nộp rồi.
xét mọi số chính phương đều có thể viết dưới dạng :
\(\left(a\cdot n+b\right)^2\) với mọi số \(a,b\) là các số tự nhiên và b nhở hơn n
mà ta có :
\(\left(a\cdot n+b\right)^2=a^2\cdot n^2+2ab\cdot n+b^2\equiv b^2mod\left(n\right)\)
vậy \(b^2< n\forall b< n\)điều này chỉ đúng khi n=2
vậy n=2
Bài gì mà khó dọ!;-;
Xem thêm câu trả lời





















