có 15 quyển sách trong đó có 7 quyển toán,3 quyển lí, 5 quyển văn. tính xác suất để lấy được :
a) 2 quyển toán
b) 1 quyển văn và 1 quyển lí
c) 2 quyển trong đó có ít nhất 1 quyển văn
Có 15 quyển sách trong đó có 7 quyển sách Toán,5 quyển sách Văn và 3 quyển sách Lý.Tính xác suất để lấy được:
a) Hai quyển sách Toán.
b) Hai quyển sách trong đó có 1 quyển Văn và 1 quyển L ý.
c) Hai quyển sách trong đó có ít nhất 1 quyển Văn.
a, Hai quyển sách toán: 7/15 x 7/15
b, Hai quyển sách có 1 văn và 1 lý: 5/15 x 3/15 = 1/3 x 1/5= 1/15
c, Hai quyển sách ít nhất 1 quyển văn: 5/15 x 10/15 + 5/15 x 5/15
có 15 quyển sách trong đó có 7 quyển toán,3 quyển lí, 5 quyển văn. tính xác suất để lấy được :
a) 2 quyển toán
b) 1 quyển văn và 1 quyển lí
c) 2 quyển trong đó có ít nhất 1 quyển văn
Xếp 10 quyển sách tham khảo khác nhau gồm: 1 quyển sách Văn, 3 quyển sách tiếng Anh và 6 quyển sách Toán (trong đó có hai quyển Toán T1 và Toán T2) thành một hàng ngang trên giá sách. Tính xác suất để mỗi quyển sách Tiếng Anh đều được xếp ở giữa hai quyển sách Toán, đồng thời hai quyển Toán T1 và Toán T2 luôn xếp cạnh nhau.
A. 1 210 .
B. 1 600 .
C. 1 300 .
D. 1 450 .
Đáp án A.
Phương pháp giải: Áp dụng các quy tắc đếm cơ bản trong bài toán sắp xếp đồ vật
Lời giải: Xếp 5 quyển Toán (coi Toán T1 và Toán T2 là một) có 5!.2! = 240 cách.
Khi đó, sẽ tạo ra 4 khoảng trống kí hiệu như sau: _T_T_T_T_T_
Xếp 3 quyển sách Tiếng Anh vào 4 khoảng trống giữa hai quyển toán có A 4 3 cách.
Xếp 1 quyển sách Văn vào 3 vị trí còn lại có 3 cách.
Vậy xác suất cần tính là P = 240 . A 4 3 . 3 10 ! = 1 210 .
Xếp 10 quyển sách tham khảo khác nhau gồm: 1 quyển sách Văn, 3 quyển sách tiếng Anh và 6 quyển sách Toán (trong đó có hai quyển Toán T1 và Toán T2) thành một hàng ngang trên giá sách. Tính xác suất để mỗi quyển sách Tiếng Anh đều được xếp ở giữa hai quyển sách Toán, đồng thời hai quyển Toán T1 và Toán T2 luôn xếp cạnh nhau
A. 1 210
B. 1 600
C. 1 300
D. 1 450
Đáp án A
Phương pháp giải: Áp dụng các quy tắc đếm cơ bản trong bài toán sắp xếp đồ vật
Lời giải: Xếp 5 quyển Toán (coi Toán T1 và Toán T2 là một) có 5 ! .2 ! = 240 cách.
Khi đó, sẽ tạo ra 4 khoảng trống kí hiệu như sau: _T_T_T_T_T_
Xếp 3 quyển sách Tiếng Anh vào 4 khoảng trống giữa hai quyển toán có A 4 3 cách.
Xếp 1 quyển sách Văn vào 3 vị trí còn lại có 3 cách.
Vậy xác suất cần tính là P = 240. A 4 3 .3 10 ! = 1 210 .
Xếp 10 quyển sách tham khảo khác nhau gồm: 1 quyển sách Văn, 3 quyển sách tiếng Anh và 6 quyển sách Toán (trong đó có hai quyển Toán T1 và Toán T2) thành một hàng ngang trên giá sách. Tính xác suất để mỗi quyển sách tiếng Anh đều được xếp ở giữa hai quyển sách Toán, đồng thời hai quyển Toán T1 và Toán T2 luôn được xếp cạnh nhau.
A. 1 210
B. 1 600
C. 1 300
D. 1 450
HD: Xếp 10 quyển sách tham khảo thành một hàng ngang trên giá sách có : 10! cách sắp xếp.
Sắp xếp 2 cuốn toán 1 và toán 2 cạnh nhau có 2! cách,
Sắp xếp 6 cuốn sách Toán sao cho có hai quyển Toán T1 và Toàn T2 cạnh nhau có 2!.5! cách.
Khi đó có 4 vị trí để sắp xếp 3 cuốn Anh ở giữa hai quyển Toán và 3 cách sắp xếp cuốn Tiếng Anh.
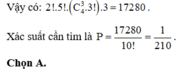
Trên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa. Lấy ngẫu nhiên 3 quyển sách. Tính xác suất để 3 quyển lấy ra có ít nhất 1 quyển là môn toán.
A. 5 42
B. 2 7
C. 1 21
D. 37 42
Trên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa. Lấy ngẫu nhiên 3 quyển sách. Tính xác suất để 3 quyển lấy ra có ít nhất 1 quyển là môn toán.
A. 5 42
B. 2 7
C. 1 21 .
D. 37 42 .
Trên giá sách có 4 quyển sách Toán, 3 quyển sách Lí và 2 quyển sách Hóa. Lấy ngẫu nhiên 3 quyển sách. Tính xác suất sao cho ba quyển lấy ra có ít nhất một quyển sách Toán.
A. 37 42
B. 5 42
C. 10 21
D. 42 37
Đáp án A
Số phần tử của không gian mẫu n Ω = C 9 3 = 84
Gọi A là biến cố sao cho ba quyển lấy ra có
ít nhất một quyển sách Toán. ⇒ n A ¯ = C 5 3 = 10
⇒ A ¯ là biến cố sao cho ba quyển lấy ra không
có sách Toán ⇒ n A ¯ = C 5 3 = 10 .
⇒ P A = 1 − P A ¯ = 1 − 10 84 = 37 42
Trên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa. Lấy ngẫu nhiên 3 quyển sách. Tính xác suất để trong ba quyển sách lấy ra có ít nhất một quyển là toán.
A. 2 7
B. 3 4
C. 37 42
D. 10 21