Cho đường tròn O đường kính AB = 2R. Từ A vẽ hai tia nằm hai bên AB và hai tia này cắt tiếp tuyến tại B ở M và N ; AM và AN cắt (O) ở C và D.
a/ Chứng Minh : tứ giác CDNM Nội tiếp
b/ Chứng Minh : AC.AM = AD.AN = 4R
c/ Cho góc CBA = 30* . Tính diện tích phần mặt phẳng của tam giác ABM nằm ngoài (O) theo R

Những câu hỏi liên quan
Cho đường tròn O đường kính AB = 2R. Từ A vẽ hai tia nằm hai bên AB và hai tia này cắt tiếp tuyến tại B ở M và N ; AM và AN cắt (O) ở C, D
a/ CM: tứ giác CDNM Nội tiếp
b/ CM: AC.AM = AD.AN = 4R^2
c/ Cho góc CBA = 30° . Tính diện tích phần mặt phẳng của tam giác ABM nằm ngoài đường tròn (O)
a: góc ACB=1/2*sđ cung AB=90 độ
=>BC vuông góc AM
góc ADB=1/2*sđ cung AB=90 độ
=>BD vuông góc AN tại D
ΔABM vuông tại B có BC là đường cao
nên AC*AM=AB^2
ΔABN vuông tại B có BD là đường cao
nên AD*AN=AB^2
=>AC*AM=AD*AN
=>AC/AN=AD/AM
=>ΔACD đồng dạng với ΔANM
=>góc ACD=góc ANM
=>góc DCM+góc DNM=180 độ
=>DCMN nội tiếp
b: AC*AM=AB^2=(2R)^2=4R^2
AD*AN=AB^2=(2R)^2=4R^2
Đúng 0
Bình luận (0)
Cho đường tròn O đường kính AB = 2R. Từ A vẽ hai tia nằm hai bên AB và hai tia này cắt tiếp tuyến tại B ở M và N ; AM và AN cắt (O) ở C và D.
a/ Chứng Minh : tứ giác CDNM Nội tiếp
b/ Chứng Minh : AC.AM = AD.AN = 2R^2
c/ Cho góc CBA = 30* . Tính diện tích phần mặt phẳng của tam giác ABM nằm ngoài (O) theo R
Cho đường tròn O đường kính AB = 2R. Từ A vẽ hai tia nằm hai bên AB và hai tia này cắt tiếp tuyến tại B ở M và N ; AM và AN cắt (O) ở C và D.
a/ Chứng Minh : tứ giác CDNM Nội tiếp
b/ Chứng Minh : AC.AM = AD.AN = 2R^2
c/ Cho góc CBA = 30* . Tính diện tích phần mặt phẳng của tam giác ABM nằm ngoài (O) theo R
Cho nửa đường tròn tâm O, đường kính AB = 2R, Ax và By là hai tiếp tuyến với nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP cắt By tại N.
Chứng minh AM.BN = R2
* Tam giác MON vuông tại O có đường cao OP nên
OP2 = MP. NP (1)
* Theo tính chất hai tiếp tuyến cắt nhau ta có
MA= MP và NB = NP (2)
Từ (1) và (2) suy ra: OP2 = MA. NB hay R2 = MA. NB ( đpcm)
Đúng 0
Bình luận (0)
Cho nửa đường tròn tâm O, đường kính AB = 2R, Ax và By là hai tiếp tuyến với nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP cắt By tại N.
Chứng minh rằng MON và APB là hai tam giác vuông đồng dạng.

a) Ta có OM, ON lần lượt là tia phân giác của AOP, BOP (tính chất của hai tiếp tuyến cắt nhau).
Mà AOP kề bù với BOP nên suy ra OM vuông góc với ON.
Vậy ΔMON vuông tại O.
Góc  là góc nội tiếp chắn nửa đường tròn nên
là góc nội tiếp chắn nửa đường tròn nên  = 900
= 900
Tứ giác AOPM có:
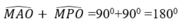
Suy ra, tứ giác AOPM nội tiếp đường tròn.
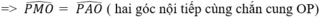
Xét ∆ MON và ∆ APB có:
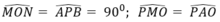
=> Hai tam giác MON và APB đồng dạng
Đúng 0
Bình luận (0)
Cho nửa đường tròn tâm O, đường kính AB 2R, Ax và By là hai tiếp tuyến với nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP cắt By tại N.Tính tỉ số
S
M
O
N
S
A
P
B
k
h
i
A
M
R...
Đọc tiếp
Cho nửa đường tròn tâm O, đường kính AB = 2R, Ax và By là hai tiếp tuyến với nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP cắt By tại N.
Tính tỉ số S M O N S A P B k h i A M = R 2
* Theo a, ∆MON và APB đồng dạng với nhau với tỉ số đồng dạng là:
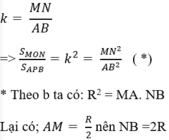
Mà: MN = MP+NP = MA+NB = R/2 +2R = 5R/2
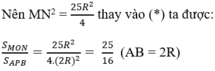
Đúng 0
Bình luận (0)
Cho đường tròn (O) đường kính AB. Vẽ tiếp tuyến Ax, với đường tròn (O) (A là tiếp điểm ). Qua C thuộc tia Ax, vẽ đường thẳng cắt đường tròn (O) tại hai điểm D và E (D nằm giữa C và E; D và E nằm về hai phía của đường thẳng AB). Từ O vẽ OH vuông góc với đoạn thẳng DE tại H.a) Chứng minh : tứ giác AOHC nội tiếp.b) Chứng minh : AC.AE AD.CEc) Đường thẳng CO cắt tia BD, tia BE lần lượt tại M và N. Chứng minh : AM//BN
Đọc tiếp
Cho đường tròn (O) đường kính AB. Vẽ tiếp tuyến Ax, với đường tròn (O) (A là tiếp điểm ). Qua C thuộc tia Ax, vẽ đường thẳng cắt đường tròn (O) tại hai điểm D và E (D nằm giữa C và E; D và E nằm về hai phía của đường thẳng AB). Từ O vẽ OH vuông góc với đoạn thẳng DE tại H.
a) Chứng minh : tứ giác AOHC nội tiếp.
b) Chứng minh : AC.AE= AD.CE
c) Đường thẳng CO cắt tia BD, tia BE lần lượt tại M và N. Chứng minh : AM//BN
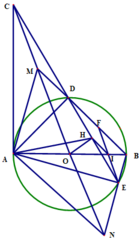
a) Ta có
C A B ⏜ = 90 0 O H C ⏜ = 90 0 ⇒ C A B ⏜ + O H C ⏜ = 180 0
Vậy tứ giác AOHC nội tiếp.
b) Ta có C A D ⏜ = A E C ⏜ , A C E ⏜ chung suy ra Δ A C D ~ Δ E C A (g.g)
⇒ C A C E = A D A E ⇒ A C . A E = A D . C E
c) Từ E vẽ đường thẳng song song với MN cắt cạnh AB tại I và cắt cạnh BD tại F ⇒ H E I ⏜ = H C O ⏜ .
Vì tứ giác AOHC nội tiếp ⇒ H A O ⏜ = H C O ⏜ = H E I ⏜ .
Suy ra tứ giác AHIE nội tiếp ⇒ I H E ⏜ = I A E ⏜ = B D E ⏜ ⇒ H I / / B D .
Mà H là trung điểm của DE=> I là trung điểm của EF. Có EF//MN và IE= IF
=> O là trung điểm của đoạn thẳng MN.
Suy ra tứ giác AMBN là hình bình hành => AM//BN.
Đúng 1
Bình luận (0)
Từ điểm A ở ngoài đường tròn (O;R) với (Oa2R) vẽ hai tiếp tuyến AB;AC đến (O)(B;C là tiếp điểm) và cắt tuyến ADE đến (O) (D nằm giữa A và E; tia AE nằm giữa hai tia AO và AB) OA cắt BC tại H;I là trung điểm DEa/Chứng minh tứ giác AIOC nội tiếp và OA vuông góc BCb/Chứng minh AB2 AD.AE và góc EDO góc EHOc/Qua D vẽ đường thẳng song song BE cắt AB;BC tại M và N.Chứng minh MDME
Đọc tiếp
Từ điểm A ở ngoài đường tròn (O;R) với (Oa>2R) vẽ hai tiếp tuyến AB;AC đến (O)(B;C là tiếp điểm) và cắt tuyến ADE đến (O) (D nằm giữa A và E; tia AE nằm giữa hai tia AO và AB) OA cắt BC tại H;I là trung điểm DE
a/Chứng minh tứ giác AIOC nội tiếp và OA vuông góc BC
b/Chứng minh AB2 = AD.AE và góc EDO= góc EHO
c/Qua D vẽ đường thẳng song song BE cắt AB;BC tại M và N.Chứng minh MD=ME
a: Xét tứ giác AIOC có \(\widehat{AIO}+\widehat{ACO}=180^0\)
nên AIOC là tứ giác nội tiếp
Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
mà OB=OC
nên OA là đường trung trực của BC
hay OA⊥BC
b: Xét ΔABD và ΔAEB có
\(\widehat{ABD}=\widehat{AEB}\)
\(\widehat{BAD}\) chung
Do đó: ΔABD\(\sim\)ΔAEB
Suy ra: AB/AE=AD/AB
hay \(AB^2=AD\cdot AE\)
Đúng 1
Bình luận (0)
Từ điểm A ở ngoài đường tròn (O;R) với (Oa2R) vẽ hai tiếp tuyến AB;AC đến (O)(B;C là tiếp điểm) và cắt tuyến ADE đến (O) (D nằm giữa A và E; tia AE nằm giữa hai tia AO và AB) OA cắt BC tại H;I là trung điểm DEa/Chứng minh tứ giác AIOC nội tiếp và OA vuông góc BCb/Chứng minh AB2 AD.AE và góc EDO góc EHOc/Qua D vẽ đường thẳng song song BE cắt AB;BC tại M và N.Chứng minh MDME
Đọc tiếp
Từ điểm A ở ngoài đường tròn (O;R) với (Oa>2R) vẽ hai tiếp tuyến AB;AC đến (O)(B;C là tiếp điểm) và cắt tuyến ADE đến (O) (D nằm giữa A và E; tia AE nằm giữa hai tia AO và AB) OA cắt BC tại H;I là trung điểm DE
a/Chứng minh tứ giác AIOC nội tiếp và OA vuông góc BC
b/Chứng minh AB2 = AD.AE và góc EDO= góc EHO
c/Qua D vẽ đường thẳng song song BE cắt AB;BC tại M và N.Chứng minh MD=ME
a: Xét tứ giác AIOC có \(\widehat{AIO}+\widehat{ACO}=180^0\)
nên AIOC là tứ giác nội tiếp
Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
mà OB=OC
nên OA là đường trung trực của BC
hay OA⊥BC
b: Xét ΔABD và ΔAEB có
\(\widehat{ABD}=\widehat{AEB}\)
\(\widehat{BAD}\) chung
Do đó: ΔABD\(\sim\)ΔAEB
Suy ra: AB/AE=AD/AB
hay \(AB^2=AD\cdot AE\)
Đúng 1
Bình luận (0)







