* Theo a, ∆MON và APB đồng dạng với nhau với tỉ số đồng dạng là:
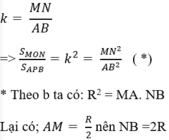
Mà: MN = MP+NP = MA+NB = R/2 +2R = 5R/2
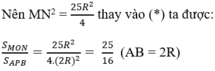
* Theo a, ∆MON và APB đồng dạng với nhau với tỉ số đồng dạng là:
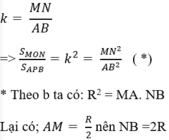
Mà: MN = MP+NP = MA+NB = R/2 +2R = 5R/2
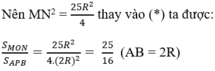
Cho nửa đường tròn tâm O, đường kính AB = 2R, Ax và By là hai tiếp tuyến với nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP cắt By tại N.
Chứng minh AM.BN = R2
Cho nửa đường tròn tâm O, đường kính AB = 2R, Ax và By là hai tiếp tuyến với nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP cắt By tại N.
Tính thể tích của hình do nửa hình tròn APB quay quanh AB sinh ra.
Cho nửa đường tròn tâm O, đường kính AB = 2R, Ax và By là hai tiếp tuyến với nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP cắt By tại N.
Chứng minh rằng MON và APB là hai tam giác vuông đồng dạng.
Cho nửa đường tròn tâm O, đường kính AB = 2R, Ax và By là hai tiêp tuyến với nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP với đường tròn tâm O (tiếp điểm P khác điểm A) cắt By tại N
a, Chứng minh các tam giác MON và APB đồng dạng
b, Chứng minh AM.BN = R 2
c, Tính tỉ số S M O N S A P B khi AM = R 2
d, Tính thể tích của hình do nửa hình tròn đường kính AB quay một vòng quanh AB sinh ra
Cho nửa đường tròn tâm O, đường kính AB = 2R, Ax và By là hai tiếp tuyến với nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP cắt By tại N.
a, Chứng minh MON và APB là hai tam giác vuông đồng dạng
b, Chứng minh AM.BN = R 2
c, Tính tỉ số S M O N S A P B khi AM = R 2
d, Tính thể tích của hình do nửa hình tròn APB quay quanh AB sinh ra
Cho nửa đường tròn tâm O, đường kính AB = 2R, Ax và By là hai tiếp tuyến với nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP cắt By tại N.
a) Chứng minh rằng MON và APB là hai tam giác vuông đồng dạng.
b) Chứng minh AM ⋅ BN = R 2
c) Tính tỉ số S M O N S ∆ D B khi A M = R 2
d) Tính thể tích của hình do nửa hình tròn APB quay quanh AB sinh ra.
Cho nửa đường tròn tâm O O, đường kính A B = 2 R AB=2R, A x Ax và B y By là hai tiếp tuyến với nửa đường tròn tại A A và B B. Lấy trên tia A x Ax điểm M M rồi vẽ tiếp tuyến M P MP cắt B y By tại N N. a) Chứng minh rằng M O N MON và A P B APB là hai tam giác vuông đồng dạng. b) Chứng minh rằng A M . B N = R^2
Cho nửa đường tròn tâm O, đường kính AB=2R, tiếp tuyến Ax,By với nửa đường tròn tâm O ( Ax, By nằm cùng phía với nửa đường tròn đó). Tiếp tuyến tại M với đường tròn tâm O ( M khác A,B) cắt Ax, By lần lượt tại C, D.
a) Chứng minh: A,C,O,M thuộc 1 đường tròn ( mik làm được rồi)
b) Chứng minh: Góc COD = 90 độ, và AC.BD = R^2
c) Gọi N là giao điểm AD và BC. Tia MN cắt AB tại H. Chứng minh N là trung điểm của HM
d) Cho S tứ giác ABCD= 20 cm^2 , Ab = 5cm. Tính diện tích tam giác ANB
cho nửa đường tròn tâm O bán kính R,đường kính AB từ A và B vẽ 2 tiếp tuyến Ax và By,1 điểm M di động trên nửa đường tròn này vẽ tiếp tuyến tại M cắt Ax và By lần lượt tại C và D.
a)tính góc COD
b)xác định vị trí của M trên nửa đường tròn O sao cho AB+BD nhỏ nhất
giúp mình với