Cho hình bên
a) Tính góc KOL
b) Kẻ tia IO, hãy tính góc KIO
c) Điểm O có cách đều ba cạnh của tam giác IKL không? Tại sao?
Cho hình 38.
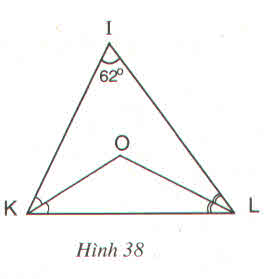
a) Tính góc KOL
b) Kẻ tia IO, hãy tính góc KIO
c) Điểm O có cách đều ba cạnh của tam giác IKL không ? Tại sao ?
Hướng dẫn:
a) ∆KIL có ˆII^ = 620
nên ˆIKL+ˆILKIKL^+ILK^ = 1180
Vì KO và LO là phân giác ˆIKLIKL^, ˆILKILK^
nên ˆOKL+ˆOLKOKL^+OLK^= 1212(ˆIKL+ˆILKIKL^+ILK^)
=> ˆOKL+ˆOLKOKL^+OLK^ = 1212 1180
ˆOKL+ˆOLKOKL^+OLK^ = 590
∆KOL có ˆOKL+ˆOLKOKL^+OLK^ = 590
nên ˆKOLKOL^ = 1800 – 590 = 1210

c) Vì O là giao điểm của hai đường phân giác của ˆKK^ và ˆLL^ nên O cách đều ba cạnh của tam giác IKL
a, Áp dụng định lí tổng 3 góc trong ΔIKL, ta có:
∠I + ∠IKL + ∠ILK= 180 độ
⇒ ∠IKL + ∠ILK= 180 độ - ∠I
OK, OL là phân giác của các góc K, L nên:
∠OKL= 1/2∠IKL, ∠OLK= 1/2∠ILK
⇒ ∠OKL + ∠OLK= 1/2 (∠IKL + ∠ILK)
= 1/2 . (180 độ - ∠I)
Áp dụng định lí tổng 3 góc trong ΔOKL có:
∠ KOL + ∠OKL + ∠OLK = 180 độ
⇒ ∠KOL= 180 độ - (∠OKL + ∠OLK)
= 180 độ - 180- ∠I / 2= 180 + ∠I/2
Mà ∠I= 62 độ nên:
∠KOL= 180 +62/2= 121 độ
b, Ta có: 3 đường phân giác trong tam giác đồng quy.
Mà 2 đường phân giác KO, LO cắt nhau tại O
⇒ OI là tia phân giác của ∠KIL
⇒ ∠KIO= 1/2 ∠KIL= 1/2. 62 độ= 31 độ
c, O là giao điểm 3 đường phân giác của ΔIKL. Áp dụng định lí 3 đường phân giác
Vậy O cách đều 3 cạnh của ΔIKL
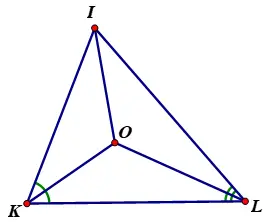
a) Áp dụng định lý tổng ba góc trong tam giác IKL ta có:
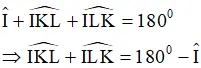
OK, OL là phân giác của các góc K, L nên
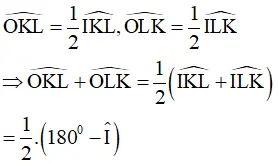
Áp dụng định lý tổng ba góc trong tam giác OKL có:
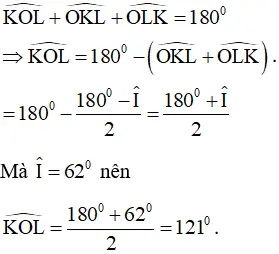
b) Ta có : ba đường phân giác trong tam giác đồng quy.
Mà hai đường phân giác KO, LO cắt nhau tại O
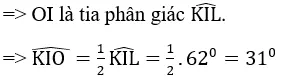
c) O là giao điểm ba đường phân giác của ΔIKL
Áp dụng định lí 3 đường phân giác
Vậy O cách đều ba cạnh của tam giác IKL.
Cho hình 38
a) Tính góc KOL
b) Kẻ tia IO , hãy tính góc KIO
c) Điểm O có cách đề ba cạnh của tam giác IKL ko? Tại sao?
HÌNH 38 SGK TOÁN 7 TẬP 2 TRANG 73
HELP ME
. Cho tam giác ABC có góc A=120 độ . Đường phân giác của góc B và góc C là BD và CE cắt nhau tại I.
a, Tính số đo của góc BIC.
b, Kẻ tia IA, hãy tính góc EAI.
c, Điểm I có cách đều ba cạnh của tam giác ABC hay không? Tại sao?
giúp mk vs:((
![]()
Bạn bổ sung đề đi bạn: Số đo của góc B và góc C là bao nhiêu???
a) Xét ΔABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)(Định lí tổng ba góc trong một tam giác)
\(\Leftrightarrow\widehat{B}+\widehat{C}=60^0\)
\(\Leftrightarrow2\left(\widehat{IBC}+\widehat{ICB}\right)=60^0\)
hay \(\widehat{IBC}+\widehat{ICB}=30^0\)
Xét ΔIBC có \(\widehat{BIC}+\widehat{IBC}+\widehat{ICB}=180^0\)(Định lí tổng ba góc trong một tam giác)
\(\Leftrightarrow\widehat{BIC}+30^0=180^0\)
hay \(\widehat{BIC}=150^0\)
Vậy: \(\widehat{BIC}=150^0\)
c) Xét ΔABC có
BD là đường phân giác ứng với cạnh AC(gt)
CE là đường phân giác ứng với cạnh AB(gt)
BD cắt CE tại I(gt)
Do đó: I là tâm đường tròn nội tiếp ΔABC
hay I cách đều ba cạnh của ΔACB
Cho hình 38.
Điểm O có cách đều ba cạnh của tam giác IKL không? Tại sao?
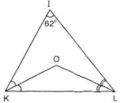
O là giao điểm ba đường phân giác của ΔIKL
Áp dụng định lí 3 đường phân giác
Vậy O cách đều ba cạnh của tam giác IKL.
Cho hình vẽ bên:
a) Tính góc KOL
b) Kẻ tia IO, hãy tính góc KIO.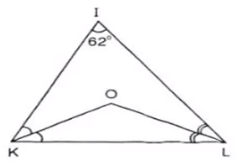
a) Áp dụng định lý tổng ba góc trong tam giác IKL ta có:
OK, OL là phân giác của các góc K, L nên
Áp dụng định lý tổng ba góc trong tam giác OKL có:
b) Ta có : ba đường phân giác trong tam giác đồng quy.
Mà hai đường phân giác KO, LO cắt nhau tại O
Cho tam giác ABC có góc A=70 độ.Vẽ đường p/giác ở góc B và góc C cắt nhau tại O.
a)Tính góc BOC
b)Kẻ tia AO.Hãy tính góc BAO
c)Điểm O có cách đều 3 cạnh của tam giác ABC.Vì sao?
Cho tam gác ABC, góc A= 64 độ , tia phân giác của góc B và góc C cắt nhau tại I
a) Tính góc BIC
b) Kẻ AI. Tính góc BAI
c) điểm I có cách đều 2 cạnh của tam giác không? Vì sao?
cho tam giác ABC có góc A = 70 độ. họi O là giao điểm của 2 đường phân giác xuất phát từ điểm B và C.
a, Tính góc BOC
b,Kẻ tia AO. hãy tính góc BAO
c, Điểm O có cách đều 2 cạnh của tam giác ABC hay không
Cho tam giác ABC co góc BAC=50\(^o\).O là giao diểmcuar 2 tia phân giác cua góc B và C.
a) Tính góc BOC
b)Điểm O có cách đều 3 cạnh của tam giác không?Tại sao
c) Kẻ tia AD.Tính góc BAO
HUHU CÁC BẠN GIÚP MÌNH NHA MAI MÌNH THI RÙI
a) Ta có : góc ABC + góc ACB= 130 độ (tự chứng minh)
=> 2 lần góc OBC + 2 lần góc OCB = 130 độ
=> 2 (góc OBC + góc OCB) = 130 độ
=> góc OBC + góc OCB = 65 độ
Xét tam giác OBC có : góc OBC + góc OCB = 65 độ
=> góc BOC = 180 độ - 65 độ = 115 độ