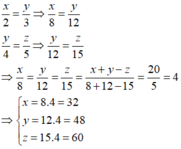Lời giải:
Ta thấy:

$(-x^2y^3)^2\geq 0$ với mọi $x,y$

$(2y^2z^4=2(yz^2)^2\geq 0$ với mọi $y,z$

$\Rightarrow (2y^2z^4)^3\geq 0$ với mọi $y,z$
Do đó để tổng $(-x^2y^3)^2+(2y^2z^4)^3=0$ thì:

$-x^2y^3=2y^2z^4=0$

Hay $(x,y,z)=(x,0,z)$ với $x,z$ bất kỳ hoặc $(x,y,z)=(0,y,0)$ với $y$ là số bất kỳ.

Ta có: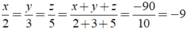 

Khi đó ta có: x = -18 ; y = -27 ; z = -45

Số lớn nhất là -18

Chọn đáp án C.

Theo đề bài ta có :

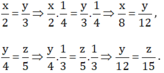
Do đó ta có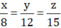 

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

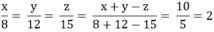
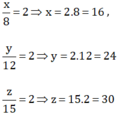
Vậy x =16 ; y = 24 ; z =30

Đáp án A

Vì x, y, z là các số nguyên dương nên x,y,z \(\ge1\)

Ta có

\(x^2+y^3+z^4=90\)

\(\Rightarrow z^4< 90\)

Ta thấy rằng \(\hept{\begin{cases}4^4=256>90\\3^4=81< 90\end{cases}}\)nên z không thể lớn hơn 4 được

Hay z nhận các giá trị là 1, 2, 3

Với z = 3 thì

\(x^2+y^3=90-3^4=9\)

Tương tự như trên ta cũng thấy được: y chỉ thể nhận các giá trị 1,2

Thế vô lần lược tìm được: y = 2, x = 1

Xét lần lược các trường hợp của z sẽ tìm được các nghiêm còn lại

Các bộ số cần tìm là: \(\left(x,y,z\right)=\left(1,2,3\right);\left(5,4,1\right);\left(9,2,1\right)\)

Mình chỉ hướng dẫn bạn cách làm thôi nhé.

Vì x,y,z là các số nguyên dg nên x,y,z >/1 

Ta có : x² +y³ +z⁴ = 90

Suy ra z⁴ < 90

Ta thấy rằng {4² = 256 > 90 , 3⁴ = 81 < 90 nên z ko thể >4

Hay z nhận các gt là 1,2,3

Với z=3 thì :

x²