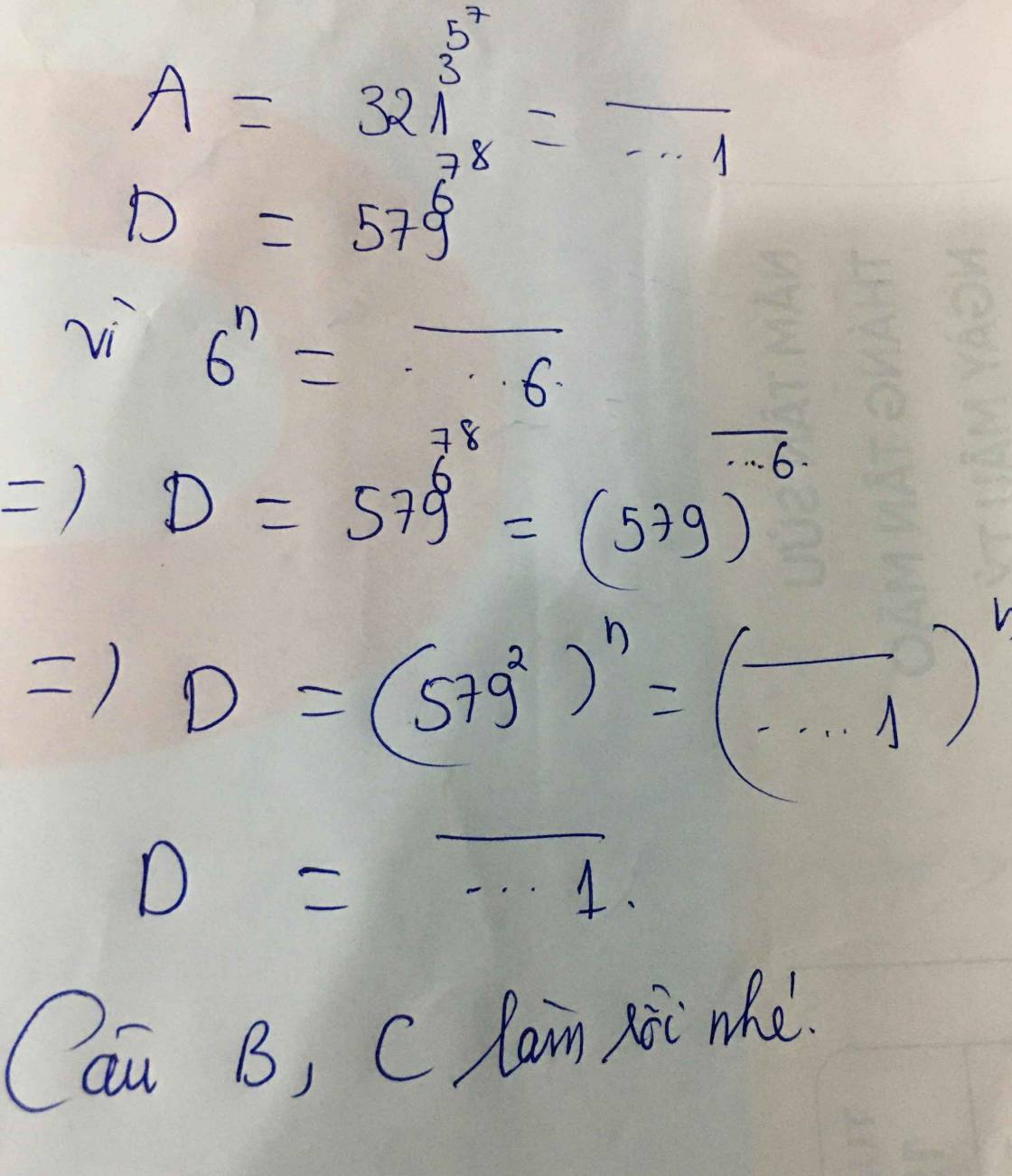Số 3 mũ 2022 có chữ số tận cùng là :A.5 .B.9 .C.3. D.1.

Những câu hỏi liên quan
Số 3 mũ 2022 có chữ số tận cùng là :A.5 .B.9 .C.3. D.1.
Tìm chữ số tận cùng của A , biết A = 1^1+ 2^5+ 3^9+ 4^13+...+504^2013+ 505^2017
gợi ý:
Số mũ có dạng 41c+ 1 ( 1c thuộc N )
=> chữ số tận cùng của A là chữ số tận cùng của tổng:
1+ 2+ 3+ 4+...+ 504+ 505 =...5
=> A có tận cùng là 5
a) Tích A= 2 . 2 mũ 2 . 2 mũ 3 ....2 mũ 10 . 5 mũ 2 . 5 mũ 4 . 5 mũ 6 ...5 mũ 14. có tận cùng bn chữ số 0 ?
b Tìm c/s tận cùng của
M= 11 ! ; N= 17 ! ; P=(2.4.6...98)+(1.3.5.7+...99); Q= 22022; K= 31993
tìm chữ số tận cùng của các số sau :
a) 321^3^5^7 b) 2022^2022
c) 234^5^6^7 d) 579^6^7^8
S=2 mũ 1+3 mũ 5+4 mũ 9 +.......+2014 mũ 8049 có chữ số tận cùng là
lũy thừa 16 mũ 137 có chữ số tận cùng là
a.6 b.3 c.9 d.2
Trả lười :
Lũy thừa của 16137 có tận cùng là :
A.6 B.3 C. 9 D.2
trả lời
a.6 nha bạn
hok tốt
Trả lời:
Lũy thừa 16137 có chữ số tận cùng là
a.6 b.3 c.9 d.2
Xem thêm câu trả lời
a) Các số có chữ số tận cùng là 0, 1, 5, 6 khi nâng lên lũy thừa bậc bất kì thì chữ số tận cùng vẫn không thay đổi.b) Các số có chữ số tận cùng là 4, 9 khi nâng lên lũy thừa bậc lẻ thì chữ số tận cùng vẫn không thay đổi.c) Các số có chữ số tận cùng là 3, 7, 9 khi nâng lên lũy thừa bậc 4n (n thuộc N) thì chữ số tận cùng là 1.d) Các số có chữ số tận cùng là 2, 4, 8 khi nâng lên lũy thừa bậc 4n (n thuộc N) thì chữ số tận cùng là 6
Đọc tiếp
a) Các số có chữ số tận cùng là 0, 1, 5, 6 khi nâng lên lũy thừa bậc bất kì thì chữ số tận cùng vẫn không thay đổi.
b) Các số có chữ số tận cùng là 4, 9 khi nâng lên lũy thừa bậc lẻ thì chữ số tận cùng vẫn không thay đổi.
c) Các số có chữ số tận cùng là 3, 7, 9 khi nâng lên lũy thừa bậc 4n (n thuộc N) thì chữ số tận cùng là 1.
d) Các số có chữ số tận cùng là 2, 4, 8 khi nâng lên lũy thừa bậc 4n (n thuộc N) thì chữ số tận cùng là 6
A = 7 + 7mũ 2 + 7 mũ 3 + ... + 7 mũ 8
a) Số A là số chẵn hay số lẽ ?
b) Số A có chia hết cho 5 không ?
c) Chữ số tận cùng của A là chữ số nào ?
Cho stn n thỏa mãn n mũ 9012 có tận cùng là 9, tìm c/s tận cùng của n mũ 2022
Số tự nhiên n thỏa mãn \(n^k\left(k\inℕ^∗\right)\) có tận cùng là 9 khi và chỉ khi \(n\) có chữ số tận cùng là 3, 7 hoặc 9.
TH1: Nếu \(n\) có chữ số tận cùng là \(3\) thì ta có nhận xét là \(n^{4k}\) có chữ số tận cùng là 1 với mọi số tự nhiên \(k\). Thật vậy, với \(k=0\) thì \(n^0=1\) có tận cùng là 9. Giả sử khẳng định đúng đến \(k=l\). Với \(k=l+1\) thì \(n^{4\left(l+1\right)}=n^{4l+4}=n^4.n^{4l}=\overline{A1}.\overline{B1}\) có chữ số tận cùng là 1. Vậy khẳng định được chứng minh. Do đó, \(n^{9012}=n^{4.2253}\) có chữ số tận cùng là 1, không thỏa ycbt.
TH2: \(n\) có chữ số tận cùng là 7 thì làm tương tự với TH1, \(n^{4k}\) luôn có chữ số tận cùng là 7 nên không thỏa ycbt.
TH3: \(n\) có chữ số tận cùng là 9 thì \(n^{2k}\) luôn có chữ số tận cùng là 1. Như vậy, không thể có số tự nhiên \(n\) nào thỏa mãn ycbt.
Đúng 3
Bình luận (0)