giúp mình le len với

Bài 1: 

Xét tứ giác ABCD:

\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^{o}\) (Tổng các góc trong tứ giác).

Mà \(\widehat{A}= \) \(57^o;\) \(\widehat{C}=\) \(110^o;\) \(\widehat{D}=\) \(75^o\left(gt\right).\)

\(\Rightarrow\) \(\widehat{B}=\) \(118^o.\)

Bài 2: 

Xét ΔABC có 

M là trung điểm của AC

N ladf trung điểm của BC

Do đó: MN là đường trung bình

=>MN=AB/2=4(cm)

Bài 5: 

a: AM=BC/2=5(cm)

b: Xét tứ giác AEMK có

\(\widehat{AEM}=\widehat{AKM}=\widehat{KAE}=90^0\)

Do đó: AEMK là hình chữ nhật

a: MN=(AB+CD)/2=10(cm)

Xét ΔABC có

M,N lần lượt là trung điểm của AB,AC

=>MN là đường trung bình của ΔABC

=>MN//BC và \(MN=\dfrac{BC}{2}=\dfrac{8}{2}=4\left(cm\right)\)

Ta có: AB=AC

\(AM=MB=\dfrac{AB}{2}\)(M là trung điểm của AB)

\(AN=NC=\dfrac{AC}{2}\)(N là trung điểm của AC)

Do đó: \(AM=MB=AN=NC=\dfrac{AB}{2}=\dfrac{10}{2}=5\left(cm\right)\)

Kẻ AH\(\perp\)MN tại H

Ta có: AH\(\perp\)MN

CE\(\perp\)MN

Do đó: AH//CE

Ta có: ΔAMN cân tại A

mà AH là đường cao

nên H là trung điểm của MN

=>\(HM=HN=\dfrac{MN}{2}=2\left(cm\right)\)

Ta có: ΔAHN vuông tại H

=>\(AH^2+HN^2=AN^2\)

=>\(AH^2+2^2=5^2\)

=>\(AH^2=25-4=21\)

=>\(AH=\sqrt{21}\left(cm\right)\)

Xét ΔNAH vuông tại H và ΔNCE vuông tại E có

NA=NC

\(\widehat{ANH}=\widehat{CNE}\)

Do đó: ΔNAH=ΔNCE

=>\(AH=CE=\sqrt{21}\left(cm\right)\)

* Ta có:  A B 2 + A C 2 = B C 2 ( 6 2 + 8 2 = 10 2 = 100 )

Suy ra: tam giác ABC vuông tại A

⇒ AB ⊥ AC

* Lại có: MN ⊥ AB nên MN // AC.

* Vì MN // AC và M là trung điểm của BC nên N là trung điểm của AB.

Khi đó, MN là đường trung bình của tam giác ABC .

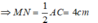
Chọn đáp án A

vẽ giúp mình hình luônn nhess

Cho 2 cái hình vì con chưa hc lp 8.

Bài 1 

 

Bài 2 : 

Bài 1:

Mượn hình bạn kia luôn nhé!

a) Vì M là trung điểm BC và MN//AB 

=> N là trung điểm của AC (tính chất của đường trung bình)

b) Vì M là trung điểm của BC, N là trung điểm của AC 

=> MN là đường trung bình của tam giác ABC

=> \(MN=\frac{1}{2}AB\)

a: Xét hình thang BDEC có 

M là trung điểm của BD

N là trung điểm của EC

Do đó: MN là đường trung bình của hình thang BDEC

Suy ra: \(MN=\dfrac{DE+BC}{2}=\dfrac{8+4}{2}=6\left(cm\right)\)

a) Ta có

+)AM=AB-BM=6-3,75=2,25

+)MN//BC => \(\frac{AN}{AC}=\frac{AM}{AB}\)=> \(\frac{AN}{8}=\frac{2,25}{6}=\frac{3}{8}\)

=> AN=3(cm)

CN=AC-AN=8-3=5(cm)

b) +)MK//BI => \(\frac{MK}{BI}=\frac{AK}{AI}\left(1\right)\)

+) NK//CI => \(\frac{NK}{CI}=\frac{AK}{AI}\left(2\right)\)

(1)(2) => \(\frac{MK}{BI}=\frac{NK}{CI}\)mà MK=NK (K là trung điểm MN)

=> BI=CI => I là trung điểm BC

c) \(\Delta\)ABC vuông tại A

=> BC²=AB²+AC²=6²+8²=10² (Định lý Pytago)

=> BC=10cm

Ta có: \(\hept{\begin{cases}\frac{AN}{CN}=\frac{3}{5}\\\frac{AB}{BC}=\frac{6}{10}=\frac{3}{5}\end{cases}\Rightarrow\frac{AN}{CN}=\frac{AB}{AC}=\frac{3}{5}}\)

=> BN là phân giác \(\widehat{ABC}\)