Giao điểm của đường thẳng d và trục tung có hoành độ x   =   0 . Thay  x   =   0 vào phương trình  y   =   3 x - 1 2  . Ta được  y   =   3 . 0   - 1 2   = 1 2

Vậy tọa độ giao điểm cần tìm là D 0 ; − 1 2

Đáp án cần chọn là: D

Giao điểm của đường thẳng d và trục tung có hoành độ  x   =   0 . Thay  x   =   0 vào phương trình y   =   2 x   +   6. Ta được  y   =   2 . 0   +   6   =   6

Vậy tọa độ giao điểm cần tìm là M (0; 6)

Đáp án cần chọn là: C

Đáp án D

Đáp án D

b) (d) cắt (P) tại 2 điểm A, B phân biệt nằm về 2 phía của trục tung khi và chỉ khi

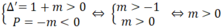
Khi đó 2 nghiệm của phương trình là:

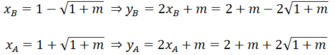
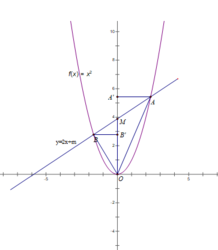
Kẻ BB' ⊥ OM ; AA' ⊥ OM

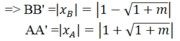
Ta có:

S A O M  = 1/2 AA'.OM ; S B O M  = 1/2 BB'.OM

Theo bài ra:

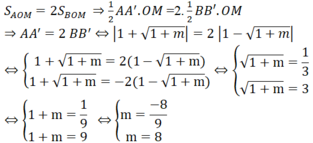
Do m > 0 nên m = 8

Vậy với m = 8 thì thỏa mãn điều kiện đề bài.

A (x; 0) là giao điểm của d với trục hoành nên  0   =   − 2 x ⇔     x   =   − 2     ⇒   A   ( − 2 ;   0 )

B (0; y) là giao điểm của d với trục tung nên  y   =   − 2 . 0   –   4     ⇔ y   =   − 4   ⇒   B   ( 0 ;   − 4 )

Suy ra  O A   =   | − 2 |   =   2 ;   O B   =   | − 4 |   =   4

Vì tam giác )AB vuông tại O nên S O A B   = O A . O B 2 = 2.4 2 = 4  (đvdt)

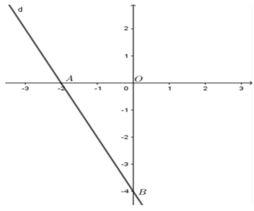
Đáp án cần chọn là: B

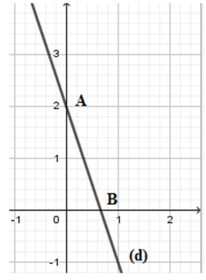
B (x; 0) là giao điểm của d với trục hoành nên 0   =   − 3 x   +   2   ⇔   x     = 2 3     B 2 3 ; 0    

A (0; y) là giao điểm của d với trục tung nên  y   =   − 3 . 0   +   2   ⇔   y   =   2 ⇒     A   ( 0 ;   2 )

Suy ra  O A   =   | 2 |   =   2 ;   O B   =     2 3 = 2 3

Vì tam giác OAB vuông tại O nên S_{OAB = O A . O B 2 = 2. 2 3 2 = 2 3}  (đvdt)

Đáp án cần chọn là: D 

1: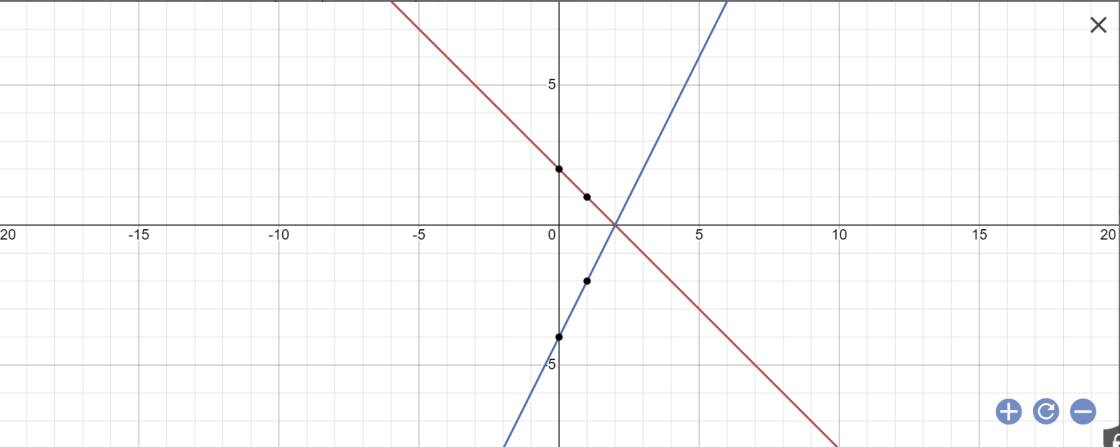 

2:Sửa đề: Gọi A là giao điểm của (d) với (d')

Tọa độ B là:

\(\left\{{}\begin{matrix}x=0\\y=-x+2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=0\\y=-0+2=2\end{matrix}\right.\)

Tọa độ C là

\(\left\{{}\begin{matrix}x=0\\y=2\cdot x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=2\cdot0-4=-4\end{matrix}\right.\)

Vậy: C(0;-4); B(0;2)

Tọa độ A là:

\(\left\{{}\begin{matrix}-x+2=2x-4\\y=2x-4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}-3x=-6\\y=2x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=2\cdot2-4=0\end{matrix}\right.\)

Vậy: A(2;0)

A(2;0); B(0;2) C(0;-4)

\(AB=\sqrt{\left(0-2\right)^2+\left(2-0\right)^2}=\sqrt{2^2+2^2}=\sqrt{8}=2\sqrt{2}\)

\(AC=\sqrt{\left(0-2\right)^2+\left(-4-0\right)^2}=\sqrt{2^2+4^2}=2\sqrt{5}\)

\(BC=\sqrt{\left(0-0\right)^2+\left(-4-2\right)^2}=6\)

Xét ΔABC có 

\(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}\)

\(=\dfrac{8+20-36}{2\cdot2\sqrt{2}\cdot2\sqrt{5}}=\dfrac{-\sqrt{10}}{10}\)

=>\(sinBAC=\sqrt{1-cos^2BAC}=\sqrt{1-\dfrac{1}{10}}=\sqrt{\dfrac{9}{10}}=\dfrac{3}{\sqrt{10}}\)

Diện tích tam giác ABC là:

\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC\)

\(=\dfrac{1}{2}\cdot2\sqrt{2}\cdot2\sqrt{5}\cdot\dfrac{3}{\sqrt{10}}=6\)