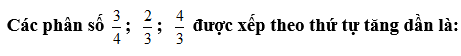\(4^3\)

Những câu hỏi liên quan
Cho A=1-3/4+(3/4)^2-(3/4)^3+(3/4)^4-(3/4)^5-.....-(3/4)^2009+(3/4)^2010
Answer:
Chứng tỏ không phải số nguyên nhỉ?
\(A=1-\frac{3}{4}+\left(\frac{3}{4}\right)^2-\left(\frac{3}{4}\right)^3+...-\left(\frac{3}{4}\right)^{2009}+\left(\frac{3}{4}\right)^{2010}\)
\(\Rightarrow A.\frac{3}{4}=\frac{3}{4}-\left(\frac{3}{4}\right)^2+\left(\frac{3}{4}\right)^3+...-\left(\frac{3}{4}\right)^{2010}+\left(\frac{3}{4}\right)^{2011}\)
\(\Rightarrow\frac{3}{4}A+A=\left(\frac{3}{4}-\left(\frac{3}{4}\right)^2+\left(\frac{3}{4}\right)^3+...-\left(\frac{3}{4}\right)^{2010}+\left(\frac{3}{4}\right)^{2011}\right)+\left(1-\frac{3}{4}+\left(\frac{3}{4}\right)^2-\left(\frac{3}{4}\right)^3+...-\left(\frac{3}{4}\right)^{2009}+\left(\frac{3}{4}\right)^{2010}\right)\)
\(\Rightarrow\frac{7}{4}A=\left(\frac{3}{4}\right)^{2011}+1\)
\(\Rightarrow A=\frac{4.\left(\frac{3}{4}\right)^{2011}+4}{7}\)
Vậy A không phải số nguyên
A 3/4; 2/3; 4/3
B 4/3; 3/4; 2/3
C 2/3; 3/4; 4/3
4/3; 2/3; 3/4
Xem thêm câu trả lời
Cho A=1-3/4+(3/4)^2-(3/4)^3+(3/4)^4-......-(3/4)^2009+(3/4)^2010
B= -3/4 + 3/ 4^2 - 3/ 4^3 + 3/4 ^4 - ... + 3/4^100
Cho A=1-3/4+(3/4)^2-(3/4)^3+(3/4)^4-......-(3/4)^2009+(3/4)^2010
A = 1 - (3/4) + (3/4)² - (3/4)³ + ... - (3/4)^2009 + (3/4)^2010
A.(3/4) = (3/4) - (3/4)² + (3/4)³ - (3/4)^4 +... - (3/4)^2010 + (3/4)^2011
cộng 2 đẳng thức trên lại vế theo vế:
A + A.(3/4) = 1 + (3/4)^2011 => 7A/4 = 1 + (3/4)^2011
=> 7A = 4 + 4.(3/4)^2011 không là số nguyên => A không nguyên
vậy A ko phải là số nguyên
Đúng 0
Bình luận (0)
cám ơn bạn... Nguyễn Phương Hiền Thảo
Thank you very much
Đúng 0
Bình luận (0)
Nguyễn Phương Hiền Thảo
Làm sao bạn biết 7A=4+4(3/4)^2011 ko phải số nguyên
Xem thêm câu trả lời
Các phân số 3/4 ; 7/7 ; 3/2 ; 4/3 được xếp theo thứ tự tăng dần là: (ghi cách giải)
A.3/4 ; 7/7 ; 3/2 ; 4/3
B.7/7 ; 4/3 ; 3/4 ; 3/2
C.3/2 ; 4/3 ; 7/7 ; 3/4
D.3/4 ; 7/7 ; 4/3 ; 3/2
Xem thêm câu trả lời
RÚT GỌN
B = 3 + 3^2 + 3^3 + 3^4 + ... + 3^50
C = 4 + 4^2 + 4^3 + 4^4 + ...+ 4^2018
\(B=3+3^2+3^3+3^4+...+3^{50}\)
\(\Rightarrow3B=3^2+3^3+3^4+3^5+...+3^{51}\)
\(\Rightarrow2B=3^{51}-3\)
\(\Rightarrow B=\frac{3^{51}-3}{2}\)
\(C=4+4^2+4^3+4^4+...+4^{2018}\)
\(\Rightarrow4C=4^2+4^3+4^4+4^5+...+4^{2019}\)
\(\Rightarrow3C=4^{2019}-4\)
\(\Rightarrow C=\frac{4^{2019}-4}{3}\)
Đúng 0
Bình luận (0)
\(B=3+3^2+3^3+...+3^{50}\)
\(\Rightarrow3B=3^2+3^3+3^4+....+3^{51}\)
\(\Rightarrow3B-B=\left(3^2+3^3+3^4+...+3^{51}\right)-\left(3+3^2+...+3^{50}\right)\)
\(\Rightarrow2B=3^{51}-3\)
\(\Rightarrow B=\frac{3^{51}-3}{2}\)
\(C=4+4^2+4^3+...+4^{2018}\)
\(\Rightarrow4C=4^2+4^3+4^4+....+4^{2019}\)
\(\Rightarrow4C-C=\left(4^2+4^3+4^4+...+4^{2019}\right)-\left(4+4^2+4^3+...+4^{2018}\right)\)
\(\Rightarrow3C=4^{2019}-4\)
\(\Rightarrow C=\frac{4^{2019}-4}{3}\)
Đúng 0
Bình luận (0)
\(B=3+3^2+...+3^{50}.\)
\(\Leftrightarrow3B=3^2+3^3+....+3^{51}\)
\(\Leftrightarrow3B-B=3^2+3^3....+3^{51}-\left(3+3^2+3^3+...+3^{50}\right)\)
\(\Leftrightarrow2B=3^{51}-3\)
\(\Leftrightarrow B=\frac{3^{51}-3}{2}\)
\(C=4+4^2+....+4^{2018}\)
\(\Leftrightarrow4C=4^2+4^3+....+4^{2019}\)
\(\Leftrightarrow4C-C=4^2+4^3+...+4^{2019}-\left(4+4^2+....+4^{2018}\right)\)
\(\Leftrightarrow3C=4^{2019}-4\)
\(\Leftrightarrow C=\frac{4^{2019}-4}{3}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
A=1-(3/4)+(3/4)^2-(3/4)^3+(3/4)^4-....-(3/4)^2009+(3/4)^2010.C/minh A ko phải số nguyên
xét B=-3/4+(3/4)^2-.......-(3/4)^n với n lẻ,n>=1
=>-3/4.B=(3/4)^2-(3/4)^3+.........+(3/4)...
trừ theo vế suy ra 7/4.B=-3/4-(3/4)^(n+1)
=>7B=-3-(3/4)^n
=>A=1+B=1-(3+(3/4)^n)/7
do <0(3/4)^n <1
suy ra 0< 3+(3/4)^n <7
suy ra (3+(3/4)^n)/7 ko là số nguyên
suy ra A ko nguyên
****
Đúng 0
Bình luận (0)
Thu gọn
B= -3/4 + 3/ 4^2 - 3/ 4^3 + 3/4 ^4 - ... + 3/4^100
\(B=-3\left(\dfrac{1}{4}-\dfrac{1}{4^2}+\dfrac{1}{4^3}-\dfrac{1}{4^4}+...-\dfrac{1}{4^{100}}\right)\)
Đặt \(C=\dfrac{1}{4}-\dfrac{1}{4^2}+...-\dfrac{1}{4^{100}}\)
\(\Leftrightarrow C\cdot\dfrac{1}{4}=\dfrac{1}{4^2}-\dfrac{1}{4^3}+...-\dfrac{1}{4^{101}}\)
\(\Leftrightarrow C\cdot\dfrac{-3}{4}=\dfrac{-1}{4^{101}}-\dfrac{1}{4}=\dfrac{-1-4^{100}}{4^{101}}\)
\(\Leftrightarrow C=\dfrac{-4^{100}-1}{4^{101}}\cdot\dfrac{-4}{3}=\dfrac{4^{100}+1}{3\cdot4^{100}}\)
\(\Leftrightarrow B=\dfrac{-4^{100}-1}{4^{100}}\)
Đúng 0
Bình luận (0)
Cho A=1-(3/4)+(3/4)*2-(3/4)*3+(3/4)*4-.....-(3/4)*2009+(3/4)*2010.
CMR: A không phải số nguyên