a; y=6/x

Giúp mik với

a,Vì x và y là 2 đại lượng tỉ lệ nghịch 

=> x1/y1 = x2/y2 = x1+x2/y1+y2 = 3+2/15 = 1/3
=>x/y = x1/y1 = 1/3
=>y=3x
 b, y=-6 
<=> -6=3x 
<=> x= -2
Vậy khi y=-6 thì x=-2

Chúc bạn học tốt nha!

a,Vì x và y là 2 đại lượng tỉ lệ nghịch 

=> x1/y1 = x2/y2 = x1+x2/y1+y2 = 3+2/15 = 1/3
=>x/y = x1/y1 = 1/3
=>y=3x

 b, y=-6 
<=> -6=3x 
<=> x= -2
Vậy khi y=-6 thì x=-2

Đáp án:

a) xy=18xy=18.

b) Khi y=−6y=−6 thì x=−3x=−3.

Giải thích các bước giải:

Gọi hệ số tỉ lệ nghịch của x và y là k Khi đó ta có

x1.y1=x2.y2=kx1.y1=x2.y2=k

⇔3y1=2y2=k⇔3y1=2y2=k

⇔y12=y23⇔y12=y23

Lại có tổng các giá trị tương ứng của y là 1515 nên ta có

y1+y2=15y1+y2=15.

Áp dụng tính chất dãy tỉ số bằng nhau ta có

y12=y23=y1+y22+3=155=3y12=y23=y1+y22+3=155=3

Suy ra y1=3.2=6,y2=3.3=9y1=3.2=6,y2=3.3=9. Từ đó tỉ lệ là

k=3y1=3.6=18k=3y1=3.6=18.

Vậy xy=18xy=18.

b) Khi y=−6y=−6, ta có

x(−6)=18x(−6)=18

⇔x=−3⇔x=−3

Vậy khi y=−6y=−6 thì x=−3x=−3.

a,Vì x và y là 2 đại lượng tỉ lệ nghịch 

=> x1/y1 = x2/y2 = x1+x2/y1+y2 = 3+2/15 = 1/3
=>x/y = x1/y1 = 1/3
=>y=3x

 b, y=-6 
<=> -6=3x 
<=> x= -2
Vậy khi y=-6 thì x=-2

a) Vì x và y là 2 đại lượng tỉ lệ nghịch

\(\Rightarrow\frac{x_1}{y_1}=\frac{x_2}{y_2}=\frac{x_1+x_2}{y_1+y_2}=\frac{3+2}{15}=\frac{5}{15}=\frac{1}{3}\)

\(\Rightarrow\frac{x}{y}=\frac{x_1}{y_1}=\frac{1}{3}\)

\(\Rightarrow y=3x\)

Vậy \(y=3x\)

b) Khi \(y=-6\)thì \(x=-2\)

Vậy khi \(y=-6\)thì \(x=-2\)

a,Vì x và y là 2 đại lượng tỉ lệ nghịch 

=> x1/y1 = x2/y2 = x1+x2/y1+y2 = 3+2/15 = 1/3
=>x/y = x1/y1 = 1/3
=>y=3x

 b, y=-6 
<=> -6=3x 
<=> x= -2
Vậy khi y=-6 thì x=-2

a,Vì x và y là 2 đại lượng tỉ lệ nghịch 

=> x1/y1 = x2/y2 = x1+x2/y1+y2 = 3+2/15 = 1/3
=>x/y = x1/y1 = 1/3
=>y=3x

 b, y=-6 
<=> -6=3x 
<=> x= -2
Vậy khi y=-6 thì x=-2

a,Vì x và y là 2 đại lượng tỉ lệ nghịch 

=> x1/y1 = x2/y2 = x1+x2/y1+y2 = 3+2/15 = 1/3
=>x/y = x1/y1 = 1/3
=>y=3x

 b, y=-6 
<=> -6=3x 
<=> x= -2
Vậy khi y=-6 thì x=-2

Hai đại lượng x và y tỉ lệ nghịch với nhau theo hệ số tỉ lệ

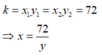
Chọn đáp án C

a: x và y là hai đại lượng tỉ lệ thuận

=>\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}\)

mà \(x_1+x_2=2;y_1+y_2=10\)

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}=\dfrac{x_1+x_2}{y_1+y_2}=\dfrac{2}{10}=\dfrac{1}{5}\)

=>\(\dfrac{x}{y}=\dfrac{1}{5}\)

=>y=5x

b: Khi x=1 thì \(y=5\cdot1=5\)