Cho tam giác abc có ba đường trung tuyến AM,BN,CP cắt nhau tại G. Chứng minh rằng:
AM+BN+CP<AB+AC+BC
Những câu hỏi liên quan
Cho tam giác ABC có ba đường trung tuyến AM, BN, CP cắt nhau tại G.
Biết AM = BN = CP. Chứng mình tam giác ABC đều.
Cho tam giác ABC có ba đường trung tuyến AM, BN, CP cắt nhau tại G. Biết AG = BG = CG. Chứng minh tam giác ABC đều
Cho tam giác ABC. Ba đường trung tuyến AM, BN, CP đồng quy tại G. Chứng minh:
\(GA + GB + GC = \dfrac{2}{3}(AM + BN + CP)\).
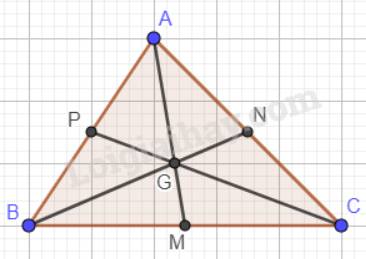
Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\)độ dài đường trung tuyến đi qua đỉnh ấy nên:
\(\begin{array}{l}\dfrac{{GA}}{{AM}} = \dfrac{{GB}}{{BN}} = \dfrac{{GC}}{{CP}} = \dfrac{2}{3}\\ \to GA = \dfrac{2}{3}AM;GB = \dfrac{2}{3}BN;GC = \dfrac{2}{3}CP\end{array}\)
Vậy:
\(GA + GB + GC = \dfrac{2}{3}AM + \dfrac{2}{3}BN + \dfrac{2}{3}CP = \dfrac{2}{3}(AM + BN + CP)\).
Đúng 0
Bình luận (0)
cho tam giác abc có 3 đường trung tuyến am,bn và cp. các đoạn thẳng cp và bn cắt nhau tại g.biết rằng ga=4cm, gb=gc=6cm
a. tính độ dài các đường trung tuyến của tam giác abc.
b. chứng minh tam giác abc cân
Cho tam giác HPG có 3 trung tuyến HM,PA,GB cắt nhau tại T . Biết TH = 3 cm,TP=TG=4 cm a, Tính HM,PA,GB. b, Chứng minh tam giác HPG cân
Đúng 0
Bình luận (0)
giúp em với ạ, em cảm ơn nhiều :
cho tam giác abc có 3 đường trung tuyến AM,BN,CP. Các đoạn thẳng CP và BN cắt nhau tại G. biết GA = 4cm. GB=GC=6cm
a) tính độ dài các đường trung tuyến của tam giác ABC
b)chứng minh tam giác ABC cân
mk pit làm phần a thui
vì AG=2GM
+) AG=4 cm
=>4=2GM
=> MG=4:2=2 (cm)
+)gm+ag=am
+)mg=2 cm
+) ag=9cm
=>2+9=am
=> am=11 cm
tính độ dài đoạn cp và bn tương tự như trên
Đúng 0
Bình luận (0)
Bài 5. Cho tam giác ABC có ba đường trung tuyến AM, BN, CP. Chứng minh rằng AM, BN, CP là độ dài ba cạnh của một tam giác.
Bài 5. Cho tam giác ABC có ba đường trung tuyến AM, BN, CP. Chứng minh rằng AM, BN, CP là độ dài ba cạnh của một tam giác.
Cho tam giác ABC, các đường trung tuyến AM, BN, CP cắt nhau tại trọng tâm G. Chứng minh:
a) SAGP = SPGB = SBGM = SMGC = SCGN = SNGA;
b) Các tam giác GAB, GBC và GCA có diện tích bằng nhau
a) Tam giác AGP và PGB có chung đường cao hạ từ đỉnh G và AP = PB nên SAGP = SPGB
Tương tự, ta có: SBGM = SMGC và SCGN = SNGA.
Vì G là trọng tâm DABC Þ AG = 2GM.
Þ SBGM = 1 2 SABG Þ SBGM = SAGP = SPGB.
Chứng minh tương tự, ta suy ra được:
SAGP = SPGB = SBGM = SMGC = SCGN = SNGA
b) Sử dụng kết quả câu a) ta có diện tích mỗi tam giác bằng 1 6 SABC, từ đó suy ra ĐPCM.
Đúng 0
Bình luận (0)
11B. Cho ABC có ba đường trung tuyến AM, BN, CP cắt nhau tại G. Biết AG = BG = CG. Chứng minh ABC đều.
Bài làm
Ta có: \(AG=\frac{2}{3}AM\)
\(CG=\frac{2}{3}CP\)
\(BG=\frac{2}{3}BN\)
Mà AG = BG = CG
=> \(\frac{2}{3}AM=\frac{2}{3}CP=\frac{2}{3}BN\)
=> \(AM=CP=BN\)
Vì AG = GC ( gt )
=> Tam giác AGC cân tại G
Mà BN là đường trung tuyến và G thuộc BN
=> GN cũng là đường trung tuyến
=> GN là đường cao ( do tam giác AGC cân ở G )
=> Tam giác ABC cân ở B
=> AB = BC (1)
Vì AG = GB ( gt )
=> Tam goác AGB cân tại G
Mà CP là đường trung tuyến và G thuộc CP
=> GN là đường trung tuyến
Và GN cũng là đường trung tuyến của tam giác cân AGC
=> GN cũng là đường cao
=> CP cũng là đường cao.
=> Tam giác ACB cân ở C
=> AC = BC (2)
Vì BG = GC ( gt )
=> Tam giác BGC cân tại G
Mà AM là đường trung tuyến và G thuộc AM
=> GM cũng là đường trung tuyến của tam giác GBC
Và GM là đường cao
=> AM cũng là đường cao
=> Tam giác ABC cân ở A
=> AB = AC (3)
Từ (1) và (2) và (3) => AB = AC = BC
=> Tam giác ABC đều.
# Học tốt #
Ta có: AG = GB (gt) => t/giác AGB cân tại G có GN là đường trung tuyến
=> GN cũng là đường cao của t/giác AGB
Hay CN là đường cao của t/giác ABC (Do C, G, N | | | )
mà CN cũng là đường trung tuyến
=> t/giác ACB cân tại C => AC = CB (1)
BG = GC (gt) => t/giác BGC cân tại G có GM là đường trung tuyến
=> GM cũng là đường cao của t/giác GBC
hay AM là đường cao của t/giác ABC (Do A; G; M | | | )
mà AM cũng là đường trung tuyến của t/giác ABC
=> t/giác ABC cân tại A => AB = AC (2)
Từ (1) và (2) => AB = AC = BC
=> t/giác ABC đều