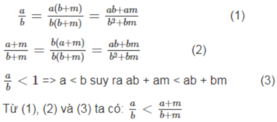cho phân số a/b(a, b thuộc N). Giả sử a/b <1 và m thuộc N, m khác ). Chứng tỏ rằng a/b<a+m/b+m

Những câu hỏi liên quan
a. Cho phân số a/b (a, b thuộc N, b≠0 ). Giả sử a/b >1 và m thuộc N . Chứng tỏ rằng a/b >a+m/b?+m
Vì \(\frac{a}{b}>1\left(a,b\inℕ,b\ne0\right)\) nên \(a>b\)
\(a>b\Rightarrow a=b+n\left(n\inℕ^∗\right)\)
Ta có : \(\frac{a}{b}=\frac{b+n}{b}=1+\frac{n}{b}\) ; \(\frac{a+m}{b+m}=\frac{b+m+n}{b+m}=1+\frac{n}{b+m}\)
Mà \(\frac{n}{b}>\frac{n}{b+m}\) nên \(1+\frac{n}{b}>1+\frac{n}{b+m}\)
hay \(\frac{a}{b}>\frac{a+m}{b+m}\) (đpcm)
cho phân số a phần b, biết a, b thuộc N, b khác 0
giả sử a phần b < 1 và m thuộc N, m khác 0. chứng tỏ rằng
\(\frac{a}{b}<\frac{a+m}{b+m}\)
cho phân số a/b(a,b thuộc N , b khác 0).
giả sử a/b < 1 và m thuộc N, m khác 0.Chứng tỏ rằng:
a/b < a+m/b+m
b
áp dụng kết quả ở câu a để so sánh 434/561 và 441/568
Cho phân số a/b (a, b ∈ N, b # 0)Giả sử a/b1 và m ∈ N, m ≠ 0. Chứng tỏ rằng:a/ba+m/b+mgiúp mình với
Đọc tiếp
Cho phân số a/b (a, b ∈ N, b # 0)
Giả sử a/b<1 và m ∈ N, m ≠ 0. Chứng tỏ rằng:
a/b<a+m/b+m
giúp mình với![]()
![]()
![]()
Cho phân số a/b (a, b ∈ N, b # 0)
Giả sử a b > 1 và m ∈ N, m ≠ 0. Chứng tỏ rằng:
a b > a + m b + m
Ta có: 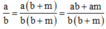
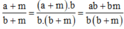
Ta có: a/b > 1 nên a > b suy ra am > bm, suy ra ab + am > ab + bm.
Do đó 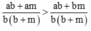
Hay 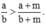
Đúng 0
Bình luận (0)
Cho phân số a/b (a, b ∈ N, b # 0)
Giả sử a b < 1 và m ∈ N, m ≠ 0. Chứng tỏ rằng:
a b < a + m b + m
1, a, cho phân số a/b thuộc N, b khác 0). Giả sử a/b <1 và m thuộc N, m khác 0. Chứng tỏ rằng: a/b < a+m/b+m
b, So sánh: 437/564 và 446/573
GIÚP MK VỚI< MK CẢM ƠN MN NHIỀU !!!!!!!!!!
Câu 1: Giải
\(\frac{a}{b}< 1\Leftrightarrow a< b\)
\(\Leftrightarrow am< bm\)
\(\Leftrightarrow ab+am< ab+bm\)
\(\Leftrightarrow a\left(b+m\right)< b\left(a+m\right)\)
\(\Leftrightarrow\frac{a}{b}< \frac{a+m}{b+m}\left(đpcm\right)\)
Câu 2: Giải
Ta có : \(\hept{\begin{cases}\frac{437}{564}=1-\frac{127}{564}\\\frac{446}{573}=1-\frac{127}{573}\end{cases}}\)
Vì \(\frac{127}{564}>\frac{127}{573}\) nên \(\frac{437}{564}>\frac{446}{573}\)
Đúng 0
Bình luận (0)
Bài 1 Tìm hai phân số khác nhau,các phấn số này lớn hơn 1/5 nhưng nhỏ hơn 1/4.Bài 2 : a) Cho phân số a/b (a,b thuộc tập hợp N , b khác 0. Giả sử a/b 1 và m thuộc tập hợp N,m khác 0 . Chứng tỏ rằng a/ba+m/b+mb) Áp dụng kết quả ở câu a) để só sánh 434/561 và 441/568Bài 3 : Cho phân số a/b (a,b thuộc tập hợp N , b khác 0. Giả sử a/b 1 và m thuộc tập hợp N,m khác 0.Chứng tỏ rằng a/ba+m/b+mb) Áp dụng kết quả ở câu a) để só sánh: 237/142 và 246/151Bài 4: So sánh : A1718+1/1719+1 và B 1717+1/1718+1B...
Đọc tiếp
Bài 1 Tìm hai phân số khác nhau,các phấn số này lớn hơn 1/5 nhưng nhỏ hơn 1/4.
Bài 2 : a) Cho phân số a/b (a,b thuộc tập hợp N , b khác 0. Giả sử a/b < 1 và m thuộc tập hợp N,m khác 0 . Chứng tỏ rằng
a/b<a+m/b+m
b) Áp dụng kết quả ở câu a) để só sánh 434/561 và 441/568
Bài 3 : Cho phân số a/b (a,b thuộc tập hợp N , b khác 0. Giả sử a/b > 1 và m thuộc tập hợp N,m khác 0.Chứng tỏ rằng
a/b>a+m/b+m
b) Áp dụng kết quả ở câu a) để só sánh: 237/142 và 246/151
Bài 4: So sánh : A=1718+1/1719+1 và B = 1717+1/1718+1
Bài 5 : So sánh : C=9899+1/9889+1 và D = 9898+1/9888+1
a) Cho phân số a/b (a, b thuộc N, b khác 0)
Giả sử a/b <1 và mà m thuộc N, m khác 0. Chứng tỏ rằng:
a/b<a+m/b+m
b) Áp dụng kết quả ở câu a) để so sánh 434/561 và 441/568