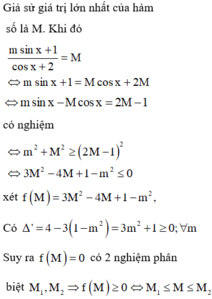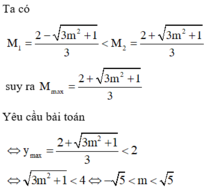tìm tích của các số nguyên lớn hơn -99 và nhỏ hơn 10
tích của 2 số nguyên có 2 chữ số phân biệt giá trị lớn nhất là bao nhiêu
cảm ơn nhiều

Những câu hỏi liên quan
tìm x thuộc Z, sao cho:
a) x + 23 là số nguyên âm lớn nhất
b) x + 99 là số nguyên âm nhỏ nhất có 2 chữ số
c) 9 bé hơn hoặc bằng | x - 3 | < 11
d) tìm giá trị nhỏ nhất và lớn nhất của x sao cho 1986 < | x + 2 | < 2015
Tìm giá trị của đa thức 0,001a3b2 - 500a2b3 trong đó a là số nguyên âm lớn nhất có 2 chữ số còn b là số nguyên nhỏ nhất,lớn hơn -5,3 và nhỏ hơn -2,5
Cho năm số nguyên phân biệt sao cho tổng của ba số nguyên bất kì trong chúng lớn hơn tổng hai số còn lại. Tìm giá trị nhỏ nhất của tích năm số nguyên đó
1) Cho A 4n+1/2n+3. Tìm n thuộc số nguyên để: a) A là 1 số nguyên của Ab) Tìm giá trị lớn nhất và nhỏ nhất của A2) Tìm số nguyên dương n nhỏ nhất sao cho ta có cách thêm n chữ số sau số đó để số chia hết cho 393) Tìm giá trị lớn nhất của thương 1 số tự nhiên có 3 chữ số và tổng các chữ số của nó4) Tìm giá trị nhỏ nhất của hiệu giữa 1 số tự nhiên có 2 chữ số và tổng ấc chữ số của nó
Đọc tiếp
1) Cho A= 4n+1/2n+3. Tìm n thuộc số nguyên để:
a) A là 1 số nguyên của A
b) Tìm giá trị lớn nhất và nhỏ nhất của A
2) Tìm số nguyên dương n nhỏ nhất sao cho ta có cách thêm n chữ số sau số đó để số chia hết cho 39
3) Tìm giá trị lớn nhất của thương 1 số tự nhiên có 3 chữ số và tổng các chữ số của nó
4) Tìm giá trị nhỏ nhất của hiệu giữa 1 số tự nhiên có 2 chữ số và tổng ấc chữ số của nó
Tìm tổng của 2 số thập phân biệt số thập phân thứ nhất cả phần nguyên là số lớn nhất có một chữ số và phần thập phân là số lớn nhất có hai chữ số khác nhau , số thứ hai hơn số thứ nhất 17,3
trong một nhóm các số nguyên dương phân biệt,số lớn nhất bé hơn 36 và bằng 3 lần số nhỏ nhất.số nhỏ nhất bằng \(\dfrac{2}{3}\) trung bình cộng của các số trong nhóm.hỏi nhóm này có tối đa bao nhiêu số?
Lời giải:
Giả sử nhóm trên có $m$ số nguyên dương phân biệt thỏa mãn, xếp theo thứ tự tăng dần là $a_1,a_2,....,a_m$
Ta có:
$a_1=\frac{2}{3}.\frac{a_1+a_2+....+a_m}{m}$
$3ma_1=2(a_1+a_2+....+a_m)$
$\geq 2[a_1+(a_1+1)+(a_1+2)+....+(a_1+m-2)+3a_1]$
$=2[(m+2)a_1+\frac{(m-1)(m-2)}{2}]=(2m+4)a_1+(m-1)(m-2)$
$\Rightarrow a_1(m-4)\geq (m-1)(m-2)$
Vì $m\geq 2$ nên $m-4\geq 0$
$a_1=\frac{a_m}{3}< \frac{36}{3}=12$
$\Rightarrow a_1\leq 11$
$\Rightarrow 11(m-4)\geq (m-1)(m-2)$
$\Leftrightarrow m^2-14m+46\leq 0$
$\Leftrightarrow -\sqrt{3}+7\leq m\leq \sqrt{3}+7$
Mà $m$ nguyên nên 6\leq m\leq 8$
Vậy $m_{\max}=8$
Ta sẽ chỉ ra bộ số thỏa mãn:
$(11,12,13,14,15,16,18,33)$
Đúng 2
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số m để giá trị lớn nhất của hàm số
y
m
sin
x
+
1
cos
x
+
2
nhỏ hơn 2? A. 5 B. 3 C. 4 D. 6
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để giá trị lớn nhất của hàm số y = m sin x + 1 cos x + 2 nhỏ hơn 2?
A. 5
B. 3
C. 4
D. 6
Đáp án A
Giả sử giá trị lớn nhất của hàm số là M. Khi đó
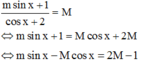
có nghiệm
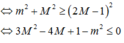
xét ![]()
Có ![]()
Suy ra ![]() có 2 nghiệm phân biệt
có 2 nghiệm phân biệt
![]()
Ta có
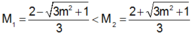
suy ra 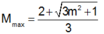
Yêu cầu bài toán
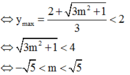
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số m để giá trị lớn nhất của hàm số
y
m
sin
x
+
1
cos
x
+
2
nhỏ hơn 2? A. 5 B. 3 C. 4 D. 6
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để giá trị lớn nhất của hàm số y = m sin x + 1 cos x + 2 nhỏ hơn 2?
A. 5
B. 3
C. 4
D. 6
| Tích của hai số nguyên có 2 chữ số phân biệt có giá trị lớn nhất là bao nhiêu? |