tim x,y biet 1/x+1/y=1/5 thanks

Những câu hỏi liên quan
tim x, y biet:
1+2y/18 = 1+4y/24 = 1+6y/6y
THANKS
Bạn làm ơn ghi rõ để ra tại có khi người khác lầm rằng
1 + 2y/18 = \(1+\frac{2y}{18}\)hay \(\frac{1+2y}{18}\)
Đúng 0
Bình luận (0)
tìm x, y mà sao chỉ có y ko còn x đâu ????
Đúng 0
Bình luận (0)
a,tim x biet |x-2|+|3-2x|=2x+1
b,tim x,y thuoc Z biet xy+2x-y=5
c, tinh A=(1-1/15)(1-1/21)(1-1/28).....(1-1/210)
tim x,y biet (x+1)(x-y)=5
Ta có :
Ư ( 5 ) = { + 1 ; + 5 }
TH1 :
x + 1 = - 1 => x = - 2
x - y = - 5 => y = 3
TH2 :
x + 1 = - 5 => x = - 6
x - y = - 1 => y = - 5
TH3 :
x + 1 = 1 => x = 0
x - y = 5 => y = - 5
TH4 :
x + 1 = 5 => x = 4
x - y = 1 => y = 3
Vậy ( x;y ) \(\in\) { ( - 2 ; 3 ) ; ( - 6 ; - 5 ) ; ( 0 ; - 5 ) ; ( 4 ; 3 ) }
Đúng 0
Bình luận (0)
tim x;y thuoc z biet:
1/x + 1/y = 1/5
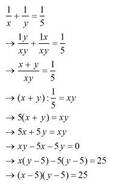
Ta xét:
\(\left(x-5\right)\left(y-5\right)=25\Leftrightarrow x-5=y-5=5\Leftrightarrow x=y=10\)
\(x-5=y-5=-5\Leftrightarrow x=y=0\)
\(\left\{{}\begin{matrix}x-5=1\\y-5=25\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\y=30\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x-5=-1\\y-5=-25\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=4\\y=-20\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x-5=25\\y-5=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=30\\y=6\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x-5=-25\\y-5=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-20\\y=4\end{matrix}\right.\)
Vậy \(\left(x,y\right)\in\left\{\left(10;10\right),\left(0;0\right),\left(6;30\right),\left(4;-20\right),\left(30;6\right),\left(-20;4\right)\right\}\)
Đúng 0
Bình luận (0)
a, tim x€Z biet (x-6) chia het cho (x-5)
b, tim x€Z, y€Z biet (x-1).(xy-5)=5
cho x,y ti le thuan tim x biet x2=3,y1=-2,y2=\(\dfrac{3}{8}\) tim x2,y2biet y2-x2=-5,x1=-6,y1=4
Vì x,y tỉ lệ thuận nên \(\dfrac{x_1}{x_2}=\dfrac{y_1}{y_2}\)
a: \(\dfrac{x_1}{x_2}=\dfrac{y_1}{y_2}\)
nên \(\dfrac{x_1}{3}=\dfrac{-2}{\dfrac{3}{8}}=-2\cdot\dfrac{8}{3}=-\dfrac{16}{3}\)
=>\(x_1=-16\)
b: \(\dfrac{x_1}{x_2}=\dfrac{y_1}{y_2}\)
\(\Leftrightarrow\dfrac{x_2}{x_1}=\dfrac{y_2}{y_1}\)
\(\Leftrightarrow\dfrac{x_2}{-6}=\dfrac{y_2}{4}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x_2}{-6}=\dfrac{y_2}{4}=\dfrac{y_2-x_2}{4-\left(-6\right)}=\dfrac{-5}{10}=-\dfrac{1}{2}\)
Do đó: \(x_2=3;y_2=-2\)
Đúng 0
Bình luận (0)
Tim x;y €z biet.
A/(x-1);(y+2)=-5
B/(x-1);(x+y)=-3
tim x va y biet
y\2=2\5+3.x=1\5+y
tim x y biet x2-5.y=x.y-4.x+1-



















