trên đường phân giác ngoài ở đỉnh C của tam giác ABC. lấy M # C. c/m AC+BC<AM+MB
có thể lm nhanh đk k
Cho tam giác ABC. Gọi d là đường phân giác của góc ngoài ở đỉnh A. Trên đường thẳng d lấy điểm M (M khác A). CMR: BA + AC < BM + MC
Trên tia đối của tia AC lấy điểm D sao cho AB = AD
=> AB + AC = AD + AC
Tam giác AMD = tam giác AMB ( c.g.c )
=> MD = MB ( 2 cạnh tương ứng )
=> MB + MC = MD + MC
Xét tam giác MCD theo bđt tam giác ta có
MD + MC > CD
=> MB + MC > AB + AC ( đpcm )
Cho tam giác ABC, d là đường phân giác góc ngoài ở đỉnh A. Trên d lấy điểm M ko trùng vs A. CMR: BA + AC < BM + MC.
1,
Cho tam giác ABC. Gọi d là đường phân giác ngoài ở đỉnh A. Trên đường thẳng d lấy điểm M khác A. Cmr:BA+AC<BM+MC
Cho tam giác ABC. Đường phân giác góc ngoài tại đỉnh B và đỉnh C của tam giác cắt nhau ở O. Từ A lần lượt kẻ đường thẳng vuông góc với hai đường phân giác trên, cắt đường thẳng BC ở M và N.
a) Chứng minh chu vi tam giác ABC bằng MN
b) Chứng minh đường trung trực của MN đi qua O
c) Chứng minh AO là tia phân giác của góc BAC
Trên đường phân giác của góc ngoài tại đỉnh C của tam giác ABC, lấy điểm D khác C. Chứng minh: DA + DB > AC + BC
Cho tam giác ABC,trung tuyến AD.Trên AD lấy E sao cho AD=DE,Trên BC lấy M sao cho BC=CM
a)Tìm trọng tâm tam giác AEM
b)Các đường phân giác góc ngoài tại đỉnh A và đỉnh C cắt nhau tại K.Chứng minh BK là tia phân giác góc ABC
Cho tam giác ABC vuông tại A. Phân giác của góc ABC cắt Ac ở E và cắt phân giác của góc ACB ở I. Trên cạnh BC lấy M sao cho IC là phân giác của EIM. Phân giác góc ngoài đỉnh B của tam giác ABc cắt CI ở K. Chứng minh rằng
a) IM vuông góc với IB
b) góc AEB= góc IMB
c) BK || IM
Cho tam giác ABC. Điểm M nằm trên đường phân giác của góc ngoài đỉnh C. Chứng minh AC + CB < AM + MB
Trên tia đối của tia CB lấy điểm A' sao cho CA' = CA. Sử dụng tính chất của tam giác cân ta có được CM là đường trung trực của AA' Þ MA = MA'. Sử dụng bất đẳng thức trong tam giác A'MB ta có: CA + CB = CA' + CB = BA' <MA' + MB Þ CA + CB < MA + MB.
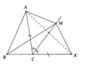
Cho tam giác ABC. Điểm M nằm trên đường phân giác của góc ngoài đỉnh C (M khác C). Chứng minh rằng AC+ CB < AM+ MB
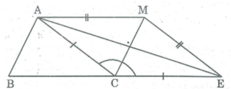
Trên tia đối tia CB lấy điểm E sao cho CE = CA. Nối MA, ME nên ∆ ACE cân tại C có CM là đường phân giác nên CM là đường trung trực (tính chất tam giác cân)
⇒ MA = ME (tính chất đường trung trực)
Ta có: AC + BC = CE + BC = BE (1)
MA + MB = ME + MB (2)
Trong ∆ MBE, ta có: BE < MB+ ME (bất đẳng thức tam giác) (3)
Từ (1), (2) và (3) suy ra: AC + CB < AM + MB.