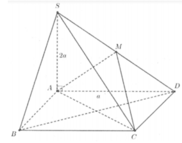
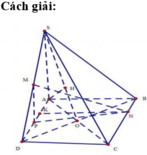
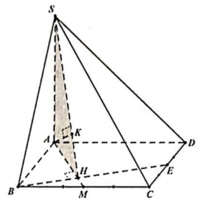
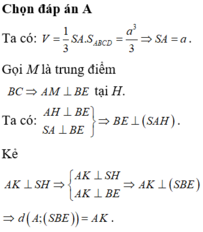Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, $BD = a$. Cạnh bên $SA = A$ vuông góc với mặt phẳng đáy. Gọi $M$, $N$ là trung điểm của $BC$ và $SD$. Tính $\tan \alpha$, biết $\alpha$ là góc giữa $MN$ và $(SAC)$.

Những câu hỏi liên quan
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tâm 0; cạnh bên SA vuông góc với mặt phẳng (ABCD) và SA=a. Gọi M,N lần lượt là trung điểm của SD và BC. Tính khoảng cách từ điểm M đến mặt phẳng (SBC)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA 2a và vuông góc với mặt phẳng đáy. Gọi M là trung điểm cạnh SD. Tang của góc tạo bởi hai mặt phẳng (AMC) và (SBC) bằng A.
3
2
B.
2
3
3
C.
5...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA = 2a và vuông góc với mặt phẳng đáy. Gọi M là trung điểm cạnh SD. Tang của góc tạo bởi hai mặt phẳng (AMC) và (SBC) bằng
A. 3 2
B. 2 3 3
C. 5 5
D. 2 5 5
Chọn D
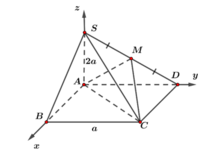
Để thuận tiện trong việc tính toán ta chọn a = 1.
Trong không gian, gắn hệ trục tọa độ Oxyz như hình vẽ sao cho gốc O trùng với điểm A, tia Ox chứa đoạn thẳng AB, tia Oy chứa đoạn thẳng AD, tia Oz chứa đoạn thẳng AS. Khi đó: A(0;0;0), B(1;0;0), C(1;1;0), S(0;0;2), D(0;1;0)
Vì M là trung điểm SD nên tọa độ là M 0 ; 1 2 ; 1
Ta có
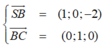
![]()
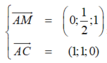
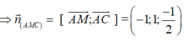
Gọi α là góc giữa hai mặt phẳng (AMC) và (SBC).
Suy ra
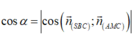
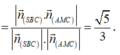
Mặt khác
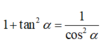
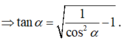
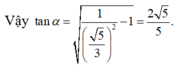
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA 2a và vuông góc với mặt phẳng đáy. Gọi M là trung điểm cạnh SD. Tang của góc tạo bởi hai mặt phẳng (AMC) và (SBC) bằng A.
5
5
B.
3
2
C.
2
5
5
D.
2...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA =2a và vuông góc với mặt phẳng đáy. Gọi M là trung điểm cạnh SD. Tang của góc tạo bởi hai mặt phẳng (AMC) và (SBC) bằng
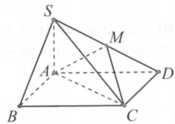
A. 5 5
B. 3 2
C. 2 5 5
D. 2 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh SA vuông góc với mặt phẳng đáy, AB=a, SA=\(a\sqrt{3}\), BC=\(a\sqrt{2}\).
a) Chứng minh BC ⊥ (SAB).
b) Gọi E là trung điểm cạnh BC. Chứng minh BD ⊥ SE.
c) Gọi \(\alpha\) là góc giữa đường thẳng SC và mặt phẳng (SBD). Tính cos \(\alpha\).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, đường thẳng SA vuông góc với mặt phẳng (ABCD). Gọi M là trung điểm của cạnh SD, N là điểm trên cạnh BC sao cho CN2BN. Biết rằng
M
N
a
10
3
tính khoảng cách từ điểm A đến mặt phẳng (SBD) theo a.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, đường thẳng SA vuông góc với mặt phẳng (ABCD). Gọi M là trung điểm của cạnh SD, N là điểm trên cạnh BC sao cho CN=2BN. Biết rằng M N = a 10 3 tính khoảng cách từ điểm A đến mặt phẳng (SBD) theo a.
![]()
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy SA
a
2
. Gọi M, N lần lượt là hình chiếu vuông góc của điểm A trên các cạnh SB, SD (tham khảo hình vẽ). Góc giữa mặt phẳng (AMN) và đường thẳng SB bằng A. 45
°
B. 60
°
C. 90
°
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy SA = a 2 . Gọi M, N lần lượt là hình chiếu vuông góc của điểm A trên các cạnh SB, SD (tham khảo hình vẽ). Góc giữa mặt phẳng (AMN) và đường thẳng SB bằng
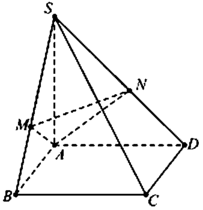
A. 45 °
B. 60 °
C. 90 °
Đáp án B
Ta có: B C ⊥ A B B C ⊥ S A ⇒ B C ⊥ M A
Mặt khác A M ⊥ S B ⇒ A M ⊥ S B C ⇒ A N ⊥ S C , tương tự A N ⊥ S C
Do đó S C ⊥ A M N , mặt khác ∆ S B C vuông tại B suy ra tan B S C ^ = B C S B = a S A 2 + A B 2 = 1 3
⇒ S B ; S C ^ = B S C ^ = 30 ° ⇒ S B ; A M N ^ = 60 ° .
Đúng 0
Bình luận (1)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Cạnh bên SA vuông góc với đáy,
S
A
2
a
3
.
Gọi I là trung điểm của mặt phẳng (P) đi qua I và vuông góc với SD. Tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng (P). A.
3
5
16
a
2
B. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Cạnh bên SA vuông góc với đáy, S A = 2 a 3 . Gọi I là trung điểm của mặt phẳng (P) đi qua I và vuông góc với SD. Tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng (P).
A. 3 5 16 a 2
B. 3 15 16 a 2
C. 15 3 16 a 2
D. 5 3 16 a 2
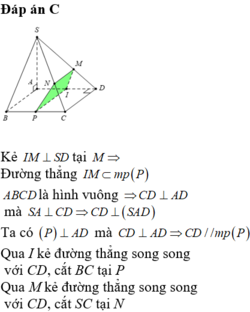
Đáp án C
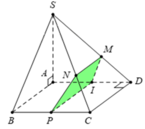
Kẻ I M ⊥ S D tại M Đường thẳng I M ⊂ m p P
ABCD là hình vuông ⇒ C D ⊥ A D mà S A ⊥ C D ⇒ C D ⊥ S A D
Ta có P ⊥ A D mà C D ⊥ A D ⇒ C D / / m p P
Qua I kẻ đường thẳng song song với CD, cắt BC tại P
Qua M kẻ đường thẳng song song với CD, cắt SC tại N
Suy ra mặt phẳng (P) cắt khối chóp S.ABCD theo thiết diện là hình thang vuông IMNP tại M và I.
Tam giác SAD vuông tại A có d A ; S D = a 3 ⇒ I M = a 3 2
Tam giác IMD vuông tại M có M D = I D 2 − I M 2 = a 2 ⇒ S M S D = 7 8 ⇒ M N = 7 a 4
Vậy diện tích hình thang IMNP là S = I M . M N + I P 2 = a 3 2 . 1 2 . 7 a 4 + 2 a = 15 3 16 a 2
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Cạnh bên SA vuông góc với đáy,SA
2
a
3
Gọi I là trung điểm của mặt phẳng (P) đi qua I và vuông góc với SD. Tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng (P).
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Cạnh bên SA vuông góc với đáy,SA= 2 a 3 Gọi I là trung điểm của mặt phẳng (P) đi qua I và vuông góc với SD. Tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng (P).
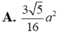
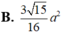
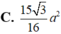

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và cạnh bên SA vuông góc với mặt phẳng đáy. Gọi E là trung điểm của cạnh CD. Biết thể tích của khối chóp S.ABCD bằng
a
3
3
. Tính khoảng cách từ A đến mặt phẳng (SBE). A.
2
a
3
B.
a
2...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và cạnh bên SA vuông góc với mặt phẳng đáy. Gọi E là trung điểm của cạnh CD. Biết thể tích của khối chóp S.ABCD bằng a 3 3 . Tính khoảng cách từ A đến mặt phẳng (SBE).
A. 2 a 3
B. a 2 3
C. a 3
D. a 3 3