Cho tam giác ABC nhọn gọi M là Trung điểm BC, D thuộc tia đôi MA: MA bằng MD. Chứng minh: tam giác ABM bằng tam giác DCM. Chứng minh DC song song với AB . Kẻ Dx vuông góc với BC tại H. K thuộc tia Dx: HK bằng HD chứng minh : MK bằng DK và AK vuông góc với DK

Những câu hỏi liên quan
Cho tam giác ABC lấy m là trung điểm cạnh BC trên tia đối của ma lấy điểm d sao cho ma = MD A chứng minh tam giác AMB bằng tam giác DMC b) chứng minh AC song song với BD Kẻ AH vuông góc với BC dh vuông góc với BC h k thuộc BC chứng minh BK = CH Gọi I là trung điểm của AC vẽ điểm e sao cho I là trung điểm của be chứng minh c là trung điểm của de
a: Xét ΔMAB và ΔMDC có
MA=MD
góc AMB=góc DMC
MB=MC
Do đo ΔMAB=ΔMDC
b: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
nên ABDC là hình bình hành
=>AC//BD
c: Xét ΔAHB vuông tại H và ΔDKC vuông tại K có
AB=DC
góc ABH=góc DCK
Do đo: ΔAHB=ΔDKC
=>AH=DK và BK=CH
Đúng 0
Bình luận (0)
cho tam giác ABC . Gọi M là trung điểm của BC. trên tia đối của tia MA lấy điểm D sao cho MA=MD.
a) Chứng minh tam giác ABM=tam giác DCM và AB///DC
b) Kẻ BE vuông góc với AM( E thuộc AM ), CF vuông góc với DM( F thuộc DM ). Chứng minh: M là trung điểm của EF
a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMDC
=>\(\widehat{MAB}=\widehat{MDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
b: Xét ΔEMB vuông tại E và ΔFMC vuông tại F có
MB=MC
\(\widehat{EMB}=\widehat{FMC}\)(hai góc đối đỉnh)
Do đó: ΔEMB=ΔFMC
=>EM=FM
=>M là trung điểm của EF
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A (AB<AC) . Gọi M là trung điểm của BC . Trên tia đối MA lấy điểm D sao cho MA=MD
a) Chứng minh : tam giác ABM = tam giác DCM
b) Vẽ AH vuông góc với BC (H thuộc BC) . Trên tia AH lấy điểm E sao cho AE=AH
Chứng minh : tam giác EBC= tam giác ABC
Chứng minh : DE song song với BC
GIÚP MÌNH NHÉ!!!!!!!!!!!!!!!!!!!!!!!!!!
Cho tam giác ABC vuông tại A có AB nhỏ hơn AC Gọi M là trung điểm của BC trên tia đối của tia MA lấy điểm D sao cho MA MDa) Chứng minh tam giác ABM bằng tam giác DCM. từ đó suy ra AB song song CD b) Trên tia đối của tia CB lấy điểm E sao cho AD AE Gọi I là trung điểm của AE chứng minh góc CAI bằng góc CEI và tính số đo của góc CAEc) Kẻ AH vuông góc với BC sao cho H thuộc BC Qua E kẻ đường song song với AC đường thẳng này cắt đường thẳng tại F chứng minh AF BCGiúp minh nha
Đọc tiếp
Cho tam giác ABC vuông tại A có AB nhỏ hơn AC Gọi M là trung điểm của BC trên tia đối của tia MA lấy điểm D sao cho MA = MD
a) Chứng minh tam giác ABM bằng tam giác DCM. từ đó suy ra AB song song CD
b) Trên tia đối của tia CB lấy điểm E sao cho AD = AE Gọi I là trung điểm của AE chứng minh góc CAI bằng góc CEI và tính số đo của góc CAE
c) Kẻ AH vuông góc với BC sao cho H thuộc BC Qua E kẻ đường song song với AC đường thẳng này cắt đường thẳng tại F chứng minh AF = BC
Giúp minh nha
Cho tam giác ABC vuông tại A có AB AC, gọi M là trung điểm của BC,trên tia đối của tia MA lấy điểm D sao cho MA MD.a)Chứng minh :tam giác ABM tam giác DCM. Từ đó suy ra AB // CD.b)Trên tia đối của tia CD lấy điểm E sao cho CA CE, gọi I là trung điểm của AE. Chứng minh góc CAI góc CEI và tính số đo góc CAE.c)Kẻ AH vuông góc BC (H thuộc BC). Qua E kẻ Đường thẳng song song với AC, đường thẳng này cắt đường thẳng AH tại F. Chứng minh : AF BC.
Đọc tiếp
Cho tam giác ABC vuông tại A có AB < AC, gọi M là trung điểm của BC,trên tia đối của tia MA lấy điểm D sao cho MA = MD.
a)Chứng minh :tam giác ABM = tam giác DCM. Từ đó suy ra AB // CD.
b)Trên tia đối của tia CD lấy điểm E sao cho CA = CE, gọi I là trung điểm của AE. Chứng minh góc CAI = góc CEI và tính số đo góc CAE.
c)Kẻ AH vuông góc BC (H thuộc BC). Qua E kẻ Đường thẳng song song với AC, đường thẳng này cắt đường thẳng AH tại F. Chứng minh : AF = BC.
Cho tam giác ABC, vẽ điểm M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MA = MD.
a) Chứng minh: tam giác ABM bằng tam giác DCM
b) Chứng minh: AB // DC
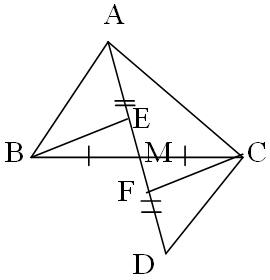
c)Kẻ BE vuông góc với AM ( E thuộc AM), CF vuông góc với DM (F thuộc DM). Chứng minh M là trung điểm của EF.
a) Xét ΔABM và ΔDCM có:
BM=CM(gt)
\(\widehat{AMB}=\widehat{DMC}\left(đđ\right)\)
AM=DM(gt)
=>ΔABM=ΔDCM(c.g.c)
b) Vì ΔABM=ΔDCM(cmt)
=>\(\widehat{ABM}=\widehat{DCM}\). Mà hai góc này pử vị trí sole trong
=>AB//DC
c)Xét ΔEBM và ΔFCM có:
\(\widehat{BEM}=\widehat{CFM}=90^o\)
BM=MC(gt)
\(\widehat{BME}=\widehat{CMF}\left(đđ\right)\)
=>ΔEBM=ΔFCM( cạnh huyền-góc nhọn)
=>ME=MF
=>M là trung điểm của EF
Đúng 10
Bình luận (4)
a) Xét ΔABM và ΔDCM, có:
MB = MC (gt)
∠AMB = ∠DCM (đối đỉnh)
MA = MD (gt)
Vậy ΔABM = ΔDCM (c-g-c)
b) Từ ΔABM = ΔDCM (chứng minh câu a)
Suy ra: ∠ABM = ∠ DCM (hai góc tương ứng)
Mà hai góc ∠ABM và ∠DCM ở vị trí so le trong
Vậy AB // DC
c) Xét ΔBEM và ΔCFM (∠E = ∠F = 90º)
Có: MB = MC (gt)
∠AMB = ∠DMC (đối đỉnh)
Do đó: ΔBEM = ΔCFM (cạnh huyền-góc nhọn)
Suy ra: ME = MF (hai cạnh tương ứng)
Vậy M là trung điểm của EF
Đúng 2
Bình luận (0)
cho tam giác ABC vuông tại A, kẻ AH vuông góc với BC(H thuộc BC), gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA. Chứng minh: a) góc ABM = góc DCM b) Tam giác ACD vuông c) MA= BC/2 d) AB^2 - AC^2 = HB^2 - HC^2
a, xét tam giác CMD và tam giác BMA có : AM = MD (gt)
MB = MC do M là trung điểm của BC (Gt)
góc CMD = góc AMB (đối đỉnh )
=> tam giác CMD = tam giác BMA (c - g - c)
=> góc ABM = góc DCM (định nghĩa)
b, góc ABM = góc DCM (Câu a) mà 2 góc này so le trong
=> CD // AB (đl)
mà CA _|_ AB do tam giác ABC vuông tại A (gt)
=> CA _|_ CD (dl)
=> góc ACD = 90 (đn)
=> tam giác ACD vuông tại C (đn)
c, xét tam giác ABC và tam giác CDA có : AC chung
góc ABC = góc CDA = 90
AB = CD do tam giác CMD = tam giác BMA (câu a)
=> tam giác ABC = tam giác CDA (2cgv)
=> AD = CB (đn)
M là trung điểm của CB => CM = 1/2BC
CM = MA
do tam giác CMD = tam giác BMA (Câu a)
=> MA = 1/2BC
d,
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có ABAC, gọi M là trung điểm của BC, trên tia đối của tia MA lấy điểm D sao cho MA MDa) Chứng minh tam giac ABM tam giác DCM. Từ đó suy ra AB//CDb)Trên tia đối của tian CD lấy điểm E sao cho CA Ce, gọi I là trung điểm của AE. Chứng minh góc CAI góc CEI và tính số đo góc CAEc) Kẻ AH vuông góc với BC (H thuộc BC). Qua E kẻ đường thẳng song song với AC, đường thẳng này cắt đường thẳng AH tại F. Chứng minh: AFBC
Đọc tiếp
Cho tam giác ABC vuông tại A có AB<AC, gọi M là trung điểm của BC, trên tia đối của tia MA lấy điểm D sao cho MA = MD
a) Chứng minh tam giac ABM = tam giác DCM. Từ đó suy ra AB//CD
b)Trên tia đối của tian CD lấy điểm E sao cho CA = Ce, gọi I là trung điểm của AE. Chứng minh góc CAI = góc CEI và tính số đo góc CAE
c) Kẻ AH vuông góc với BC (H thuộc BC). Qua E kẻ đường thẳng song song với AC, đường thẳng này cắt đường thẳng AH tại F. Chứng minh: AF=BC
cho tam giác ABC nhọn. M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MA=MD
a) chứng minh:tam giác ABM= tam giác DCM
b)chứng minh:DC//AB
c) Kẻ tia Dx vuông góc với BC tại H.Trên tia Dx lấy điểm K sao cho HK=HD.CMR:MK=MA và AK vuông góc với ĐK


















