Cho tam giác cân. Vẽ đường phân giác BD và CE
a) Chứng minh BD = CE
b) Chứng minh ED song song BC
Những câu hỏi liên quan
cho tam giác ABC có góc B bằng 60 độ vẽ phân giác Bd từ A kẻ đường thẳng vuông góc với BD cắt BD tại H và cắt BC tại E.
a) tính số đo góc BAH chứng minh tam giác ABE là tam giác cân
b) chứng minh tam giác DBA và am giác DBE
c) từ E jer đường thẳng song song với BD cắt đường thẳng BC tại F . Chứng minh tam giác ABF cân
Cho tam giác ABC cân tại A , BD là phân giác của góc ABC , CE là phân giác góc ACB
a) chứng minh BD = CE
b) Chứng minh ED song song vs BC
a)ta có tam giác ABC cân tại A suy ra AB=AC
suy ra ACB=ABC suy ra 1/2 ACB=1/2ABCsuy ra DBC=ECB=ABD=ECA
xét tam giác DBC và tam giác ECB có
BC(chung)
ABC=ACB
ABC=ACB(cmt)
suy ra tam giác DBC =ECB(g.c.g)
suy ra BD=CE
b)
xét tam giác ABD và tam giác ACE có:
AB=AC
A(chung)
ABD=ECD(theo câu a)
suy ra tam giác ABD=ACE(g.c.g)
suy ra AE=AD suy ra tam giác AED cân tại A suy ra AED=(180-A)/2(1)
ta có tam giác ABC cân tại A suy ra ABC=(180-A)/2(2)
từ (1)(2) suy ra AED=ABC
suy ra ED//BC(2 góc đồng vị)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại A, kẻ d đi qua A không cắt đoạn BC (không cắt đoạn thôi chứ không phải song song). Từ B và C kẻ BD và CE cùng vuông góc với d
a) Chứng minh BC // CE
b) Chứng minh tam giác ADB bằng tam giác CEA
c) Chứng minh BD + CE = DE
d) Gọi M là trung điểm BC. Chứng minh tam giác DAM = tam giác ECM và tam giác DME vuông cân
Cho tam giác ABC cân tại A( Góc A<90 độ).Kẻ BD vuong góc vs AC,CE vuông góc vs AB.Gọi I là giao điểm của BD và CE.
a) Chứng minhtam giác BDC= tam giác CEB
b)So sánh góc IBE và góc ICD
c)tam giác IBC là tam giác j?Vì sao?
d) Chứng minh AI vuông góc vs BC
e) CHứng minh ED song song vs BC
Cho tam giác ABC cân tại A( góc A < 90 độ ).Kẻ BD vuông góc vs AC,CE vuông góc vs AB.Gọi I là giao điểm của BD và CE.
a Chứng minh tam giấc BDC = tam giác CEB
b So sánh IBE và ICD
cTam giác IBC là tam giác j? vì sao
d Chứng minh AI vuông góc vs BC
e Chưng sminh ED song song vs BC
Cho tam giác ABC vuông tại B có góc B1=B2 ; Â=60o, kẻ BH vuông góc với AC (H thuộc AC). Qua B kẻ đường thẳng d song song với AC.
a) Tính góc ABH.
b) Chứng minh đường thẳng d vuông góc với BH.
Cho tam giác ABC vuông tại A có AB=5cm;BC=10cm.
a) Tính AC
b) Vẽ đường phân giác BD của tam giác ABCvaf gọi E là hình chiếu của D trên BC. Chứng minh tam giác ABD=tam giác EBD và AE vuông góc BD.
c) Gọi giao điểm của hai đường thẳng ED và BA là F. Chứng minh tam giác ABC=tam giác AFC
d) Qua A vẽ đường thẳng song song với BC cắt CF tại G. Chứng minh ba điểm B, D,G thẳng hàng.
SGK Toán 8 – Chân trời sáng tạo
21 tháng 7 2023 lúc 22:22
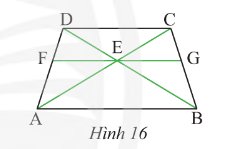
Cho hình thang cân \(ABCD\) có \(AB\) // \(CD\). Qua gia điểm \(E\) của \(AC\) và \(BD\), ta vẽ đường thẳng song song với \(AB\) và cắt \(AD\), \(BC\) lần lượt tại \(F\) và \(G\) (Hình 16). Chứng minh rằng \(EG\) là tia phân giác của góc \(CEB\).
Vì \(EG\) // \(AB\) (gt)
suy ra \(\widehat {{\rm{CEG}}} = \widehat {{\rm{CAB}}}\) (đồng vị) và \(\widehat {{\rm{GEB}}} = \widehat {{\rm{EBA}}}\) (1)
Xét \(\Delta CAB\) và \(\Delta DBA\) ta có:
\(AC = BD\) (tính chất hình thang cân)
\(BC = AD\) (tính chất hình thang cân)
\(AB\) chung
Suy ra \(\Delta CAB = \Delta DBA\) (c-c-c)
Suy ra \(\widehat {{\rm{CAB}}} = \widehat {{\rm{EAB}}}\) (2)
Từ (1) và (2) suy ra \(\widehat {{\rm{CEG}}} = \widehat {{\rm{GEB}}}\)
Suy ra \(EG\) là phân giác của \(\widehat {{\rm{CEB}}}\)
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A, BD là phân giác của góc B (D ϵ AC). Qua D, vẽ DE vuông góc với BC tại E. BD cắt AE tại H.
a/ Chứng minh ΔABE cân, suy ra H là trung điểm của AE
b/ Chứng minh DA
c/ Qua E, vẽ EF song song với BD (F ϵ AC). FH cắt ED tại G. Chứng minh ED=3GD
Cho tam giác ABC cân tại A.Vẽ các đường phân giác BD,CE
a)Chứng minh:BD=CE
b)BD cắt CE ở I.Chứng minh:tam giác BIC cân và tam giác BIE=tam giác CID
c)Chứng minh:AI vuông góc ED và ED song song với BC