Tam giác ABC có góc \(A=90^o\), \(B=30^o\)AB = 3cm. Tính các độ dài AC, BC.

Những câu hỏi liên quan
Tam giác ABC có góc A=90 độ, góc B=30 độ, AB=3cm. Tính các độ dài AC, BC.
cho tam giác góc vuông ABC(A90)có đường cao ah . biết Ab3cm và AC4cm.a chứng minh tam giác HBAcho tam giác góc vuông ABC(A90)có đường cao ah . biết Ab3cm và AC4cm.a chứng minh tam giác HBA~ AbC, B tính độ dài BC và AH AbC, B tính độ dài BC và AH
Đọc tiếp
cho tam giác góc vuông ABC(A=90)có đường cao ah . biết Ab=3cm và AC=4cm.a chứng minh tam giác HBAcho tam giác góc vuông ABC(A=90)có đường cao ah . biết Ab=3cm và AC=4cm.a chứng minh tam giác HBA~ AbC, B tính độ dài BC và AH AbC, B tính độ dài BC và AH
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
AH=3*4/5=2,4cm
Đúng 0
Bình luận (0)
a. Xét ΔHBA và ΔABC có:
\(\widehat{H}=\widehat{A}\) = 900 (gt)
\(\widehat{B}\) chung
\(\Rightarrow\) ΔHBA \(\sim\) ΔABC (g.g)
b. Vì ΔABC vuông tại A
Theo đ/lí Py - ta - go ta có:
BC2 = AB2 + AC2
BC2 = 32 + 42
\(\Rightarrow\) BC2 = 25 cm
\(\Rightarrow\) BC = \(\sqrt{25}=5\) cm
Ta lại có: ΔHBA \(\sim\) ΔABC
\(\dfrac{AH}{CA}=\dfrac{BA}{BC}\)
\(\Leftrightarrow\dfrac{AH}{4}=\dfrac{3}{5}\)
\(\Rightarrow\) AH = 2,4 cm
Đúng 0
Bình luận (0)
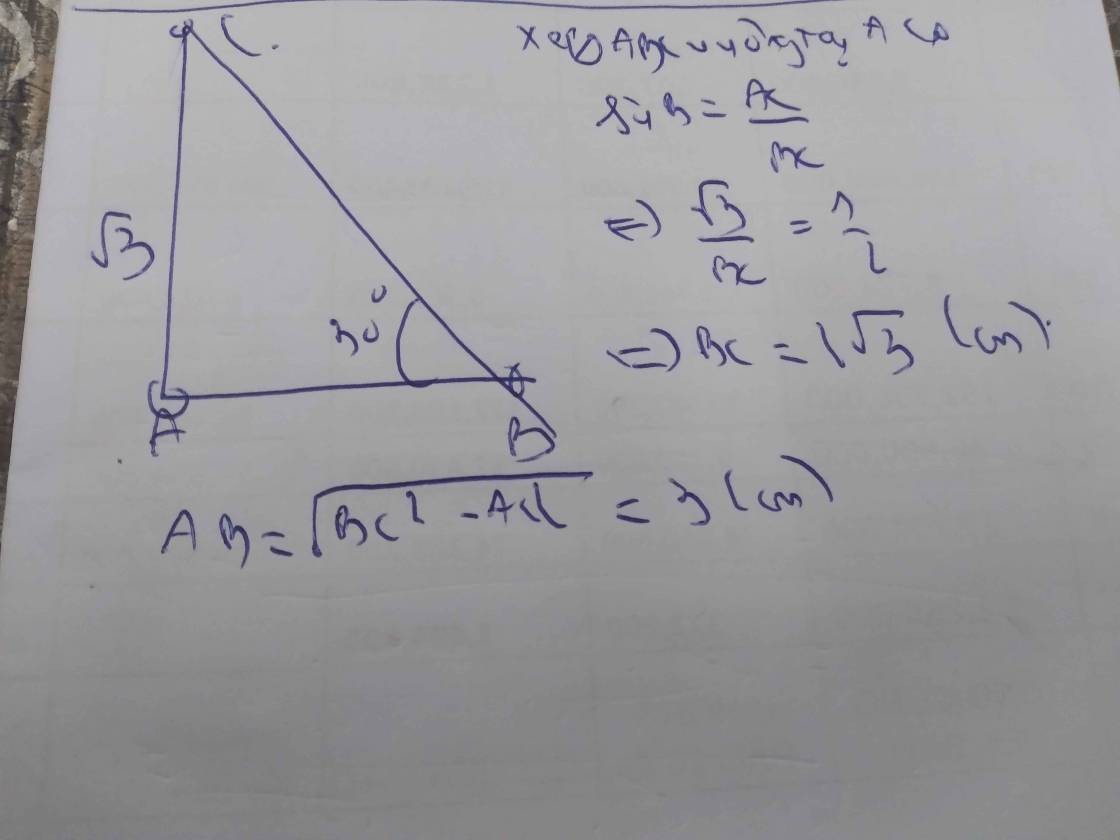
Cho tam giác ABC vuông tại A,có góc B=30 độ,AC= \(\sqrt{3cm}\).Tính độ dài các cạnh BC và AB giúp mik vs các bạn
Xem chi tiết
Cho tam giác ABC, kẻ AH vuông góc với BC. Biết AB = 5cm, BH = 3cm, BC = 10cm
a) Biết góc C = 30o. Tính góc HAC
b) Tính độ dài các cạnh AH, HC, AC
Cho tam giác ABC có Â = 90°, AB = 3cm và AC = 4 cm . Đường cao AH (H thuộc BC) a, chứng minh tam giác ABC đồng dạng tam giác HAC b, chứng minh AC² = BC.HC c,Tia phân giác góc A cắt BC tại D. Tính độ dài các đoạn thẳng BC , DB
a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
góc C chung
Do đó: ΔABC\(\sim\)ΔHAC
b: Ta có: ΔABC\(\sim\)ΔHAC
nên AC/HC=BC/AC
hay \(AC^2=BC\cdot HC\)
c: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
Đúng 0
Bình luận (0)
a, Xét Δ ABC và Δ HAC, có :
\(\widehat{ACB}=\widehat{HCA}\) (góc chung)
\(\widehat{BAC}=\widehat{AHC}=90^o\)
=> Δ ABC ∾ Δ HAC (g.g)
b, Ta có : Δ ABC ∾ Δ HAC (cmt)
=> \(\dfrac{AC}{HC}=\dfrac{BC}{AC}\)
=> \(AC^2=BC.HC\)
c, Xét Δ ABC, có :
\(BC^2=AB^2+AC^2\) (định lí Py - ta - go)
=> \(BC^2=3^2+4^2\)
=> \(BC^2=25\)
=> \(BC=5\left(cm\right)\)
Đúng 0
Bình luận (0)
Đề bài: Cho tam giác vuông ABC có góc A 90 độ, BC 2A. Gọi O là trung điểm của BC, dựng AH vuông góc với BC.a. Khi góc ACB 30 độ, tính độ dài các cạnh còn lại của tam giác.b. Khi góc ACB 30 độ, gọi M là trung điểm của AC. Tính độ dài BM.c. Khi góc ACB 30 độ, các đoạn thẳng AO và BM cắt nhau tại điểm G. Tính độ dài GC.Giúp mình với tối nay mình cần rồi, cảm ơn trước ạ.❤
Đọc tiếp
Đề bài: Cho tam giác vuông ABC có góc A = 90 độ, BC = 2A. Gọi O là trung điểm của BC, dựng AH vuông góc với BC.
a. Khi góc ACB = 30 độ, tính độ dài các cạnh còn lại của tam giác.
b. Khi góc ACB = 30 độ, gọi M là trung điểm của AC. Tính độ dài BM.
c. Khi góc ACB = 30 độ, các đoạn thẳng AO và BM cắt nhau tại điểm G. Tính độ dài GC.
Giúp mình với tối nay mình cần rồi, cảm ơn trước ạ.❤
a, Khi ![]() thì tam giác ABC là tam giác nửa đều nên
thì tam giác ABC là tam giác nửa đều nên  ,
,
![]() .
.
b, Theo câu a) ta có: 
 .
.
c. Do G là trọng tâm của tam giác ABC nên  (với N là trung điểm của AB).
(với N là trung điểm của AB).
Áp dụng định lí Pitago ta có:  . Suy ra
. Suy ra  .
.
d. Ta có:  . Diện tích tam giác AHO lớn nhất khi và chỉ khi
. Diện tích tam giác AHO lớn nhất khi và chỉ khi ![]() . Tức là AHO vuông cân tại H. Suy ra
. Tức là AHO vuông cân tại H. Suy ra ![]()
e. Tứ giác AMON là hình chữ nhật nên ![]() . Theo bất đẳng thức Côsi ta có:
. Theo bất đẳng thức Côsi ta có:
![]() . Mà
. Mà ![]() nên
nên  . Vậy
. Vậy  . Dấu bằng xảy ra khi và chỉ khi
. Dấu bằng xảy ra khi và chỉ khi ![]() , hay tam giác ABC vuông cân tại A.
, hay tam giác ABC vuông cân tại A.
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc B = 90 độ, góc A = 30 độ, BC = 3cm, đường cao BH
a, Tính AB, AC, góc C
b, Tính diện tích tam giác ABH
c, Tính bán kính đường tròn ngoại tiếp tam giác ABC
d, Tính AG ( G là trọng tâm tam giác ABC )
a, tam giác ABC vuông tại B có góc A = 30 độ => AC = 2 BC = 2. 3 = 6 cm
theo định lí Pytago ta có AB = \(\sqrt{ÃC^2-BC^2}=\sqrt{6^2-3^2}\) = \(3\sqrt{3}\) cm
góc C = 90 - 30 = 60 độ
b, tam giác ABH vuông tại H có góc A = 30 độ => AB = 2 BH => BH = \(\frac{3\sqrt{3}}{2}\)cm
theo định lí Pytago ta có AH = \(\sqrt{AB^2-BH^2}=\sqrt{\left(3\sqrt{3}\right)^2-\left(\frac{3\sqrt{3}}{2}\right)^2}=4,5cm\)
diện tích tam giác ABH =\(\frac{1}{2}.BH.AH=\frac{1}{2}.\frac{3\sqrt{3}}{2}.4,5=\frac{27\sqrt{3}}{8}\)cm vuông
Đúng 0
Bình luận (0)
mk bận quá k lm kịp 2 câu còn lại thông cảm nha
Đúng 0
Bình luận (0)
Vẽ tam giác ABC có góc A = 90°; AC = 3cm, góc C = 60°. Trên tia đối của tia AC lấy điểm D sao cho AD = AC.
a) Chứng minh ΔABD = ΔABC
b) Tam giác BCD là tam giác gì? Vì sao?
c) Tính độ dài các đoạn thẳng BC, AB
Tam giác ABC có A ^ = 90 ° , B ^ = 30 ° , A B = 6 c m . Tính các độ dài AC, BC.