Các đường cao của tam giác ABC có độ dài bằng 60, 65, và 156. Chứng minh rằng tam giác ABC vuông.

Những câu hỏi liên quan
Các đường cao của tam giác ABC có độ dài là: 60, 65, 156. Chứng minh rằng: Tam giác ABC là tam giác vuông.
Các đường cao của tam giác ABC có độ dài là: 60, 65, 156. Chứng minh rằng: Tam giác ABC là tam giác vuông.
Giúp mình mới
1, Tính diện tích tấm giác biết độ dài 3 đường cao của tấm giác đó lần lượt là:60, 65, 156 cm
2, Tam giác ABC có đường BH bằng nửa cạnh BC. Góc A bằng 75 độ. Chứng minh tam giác ABC cân
3, Tam giác ABC có góc C bằng 90 độ, góc A bằng 30 độ, cạnh AC bằng 10 cm, CD vuông góc với AB (D thuộc AB), DE vuông góc với AC ( E thuộc AC). Tính cạnh AE
Cho tam giác ABC có BC = a, AC = b, AB = c và a2 = bc. Chứng minh rằng tam giác ABC đồng dạng với tam giác có độ dài các cạnh bằng độ dài ba đường cao của tam giác ABC.
tam giác ABC có BC=a, AC=b, AC=b, a^2=bc. chứng minh rằng tam giác ABC đồng dạng với tam giác có độ dài các cạnh bằng với độ dài ba đường cao của tam giác ABC
Gọi AH,BK,CE lần lượt là các đường cao của ΔABC
Lấy DF,DG,FG lần lượt bằng AH,BK,CE
=>AH:BK:CE=BC:AC:AB(Định lí)
=>AH/BC=BK/AC=CE/AB
=>DF/BC=DG/AC=FG/AB
=>ΔDFG đồng dạng với ΔBCA
Đúng 1
Bình luận (0)
1) Cho tam giác ABC vuông ở A và có đường cao AH,AB=5cm, AC=12cm
Tính độ dài các đoạn thẳng BC,AH
2)Cho tam giác ABC( góc A=90 độ), đường cao AH. chứng minh rằng AH2=BH.CH
Tính diện tích tam giác ABC biết răng 3 đường cao có độ dài lần lượt lad 60 ; 65 ; 156
cho tam giác góc vuông ABC(A90)có đường cao ah . biết Ab3cm và AC4cm.a chứng minh tam giác HBAcho tam giác góc vuông ABC(A90)có đường cao ah . biết Ab3cm và AC4cm.a chứng minh tam giác HBA~ AbC, B tính độ dài BC và AH AbC, B tính độ dài BC và AH
Đọc tiếp
cho tam giác góc vuông ABC(A=90)có đường cao ah . biết Ab=3cm và AC=4cm.a chứng minh tam giác HBAcho tam giác góc vuông ABC(A=90)có đường cao ah . biết Ab=3cm và AC=4cm.a chứng minh tam giác HBA~ AbC, B tính độ dài BC và AH AbC, B tính độ dài BC và AH
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
AH=3*4/5=2,4cm
Đúng 0
Bình luận (0)
a. Xét ΔHBA và ΔABC có:
\(\widehat{H}=\widehat{A}\) = 900 (gt)
\(\widehat{B}\) chung
\(\Rightarrow\) ΔHBA \(\sim\) ΔABC (g.g)
b. Vì ΔABC vuông tại A
Theo đ/lí Py - ta - go ta có:
BC2 = AB2 + AC2
BC2 = 32 + 42
\(\Rightarrow\) BC2 = 25 cm
\(\Rightarrow\) BC = \(\sqrt{25}=5\) cm
Ta lại có: ΔHBA \(\sim\) ΔABC
\(\dfrac{AH}{CA}=\dfrac{BA}{BC}\)
\(\Leftrightarrow\dfrac{AH}{4}=\dfrac{3}{5}\)
\(\Rightarrow\) AH = 2,4 cm
Đúng 0
Bình luận (0)
a)cho tam giác ABC có các đường cao BD và CE bằng nhau . Chứng minh rằng tam giác đó là một tam giác cân
b)Cho tam giác ABC cân tại A,đường cao CH cắt tia phân giác của góc A tại D. Chứng minh rằng BD vuông góc với AC
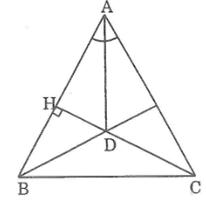
Vì ΔABC cân tại A nên đường phân giác của góc ở đỉnh A cũng là đường cao từ A.
Suy ra: AD ⊥ BC
Ta có: CH ⊥ AB (gt)
Tam giác ABC có hai đường cao AD và CH cắt nhau tại D nên D là trực tâm của ∆ABC
Suy ra BD là đường cao xuất phát từ đỉnh B đến cạnh AC.
Vậy BD ⊥ AC.
Đúng 0
Bình luận (0)
















