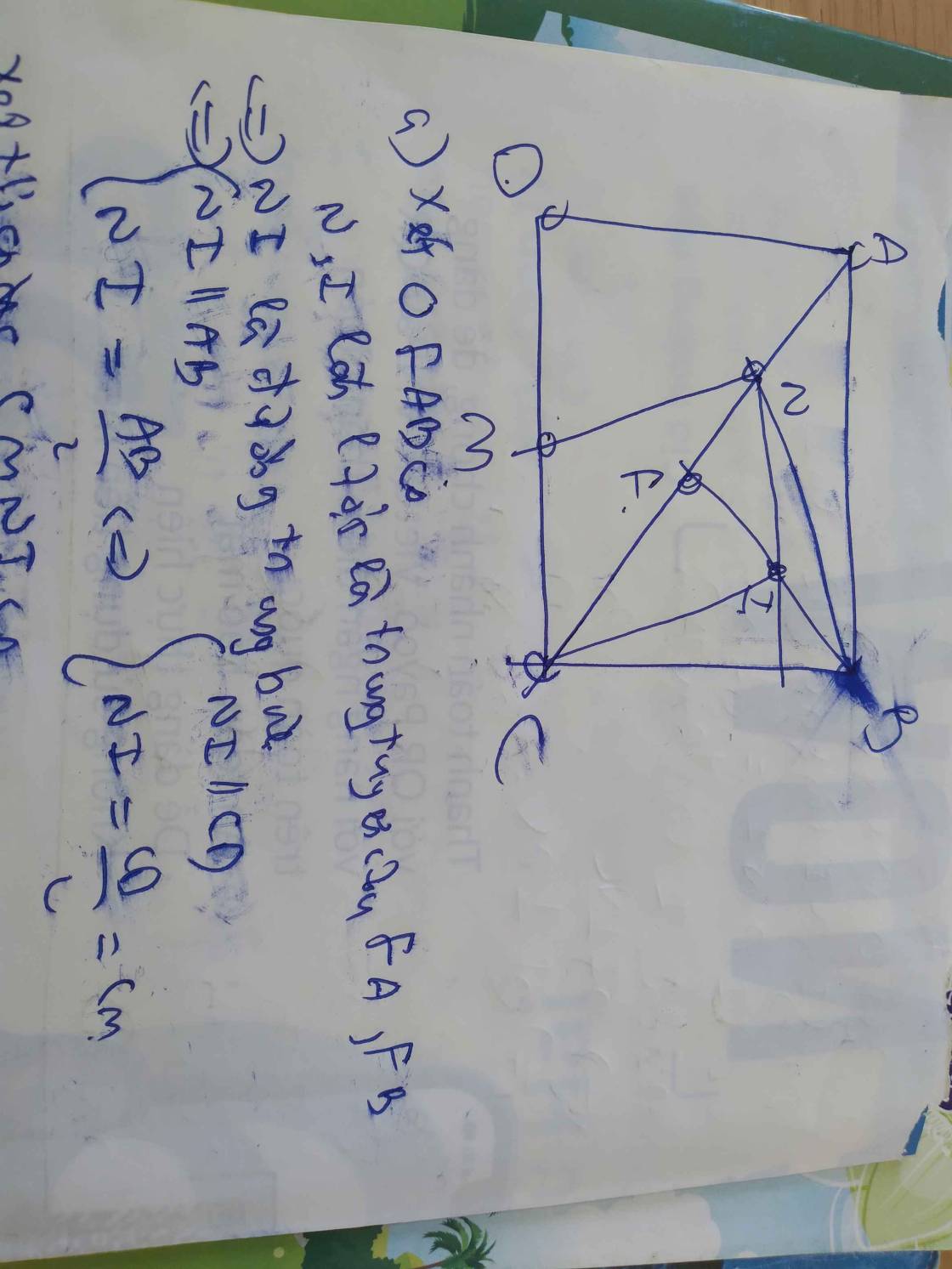
cho hình chữ nhật abcd . gọi m là trung điểm của cd và n là một điểm trên đường chéo ac sao cho góc BNM=90 độ . gọi f là điểm đối xứng của a qua n . Chứng minh rằng FB vuông góc với AC

Những câu hỏi liên quan
cho hình chữ nhật abcd .gọi m là trung điểm của cạnh cd và n là một điểm trên đường chéo ac sao cho góc bnm =90 độ .gọi f là điểm đối xứng của a qua n .cmr fb vuông góc với ac
Cho hình chữ nhật abcd, gọi M là trung điểm CD và N là điểm thuộc đường chéo AC sao cho ^BNM = 90*. Gọi F là điểm đối xứng của A qua N. CMR: FE vuông góc AC.
Cho hình chữ nhật ABCD có M là trung điểm của CD, lấy N trên AC sao cho góc BNM bằng 90 độ. Lấy điểm F đối xứng với A qua N. Gọi I là trung điểm của BF. C/m rằng
a) Tứ giác CINM là hình bình hành
b) BF vuông góc AC
Cho HCN ABCD. Gọi M là trung điểm của cạnh CD và N là một điểm trên đường chéo AC sao cho góc BNM=90 độ. Gọi F là điểm đối xứng của A qua N. CMR: FB vuông góc với AC
bạn nào cần ôn luyện toán thì cứ liên hệ mình, mình có rất nhiều bài toán nâng cao
Cho hình chữ nhật ABCD. Gọi M là trung điểm của CD, N là một điểm trên đường chéo AC sao cho BNM 90o . Gọi F là điểm đối xứng của A qua N, I là trung điểm của BF. CMR:a. Tứ giác CINM là bình bình hành. b. BF ⊥⊥AC
Đọc tiếp
Cho hình chữ nhật ABCD. Gọi M là trung điểm của CD, N là một điểm trên đường chéo AC sao cho BNM = 90o . Gọi F là điểm đối xứng của A qua N, I là trung điểm của BF. CMR:
a. Tứ giác CINM là bình bình hành.
b. BF AC
cho hình chữ nhật abcd có m là trung điểm của dc. lấy n trên ac sao cho góc bnm = 90 độ. lấy f đối xứng vs a qua n. gọi i là trung điểm của bf. cmr: a, tứ giác cinm là hình bình hành b, bf vuông góc vs ac
a)Vì A đối xứng với F qua N =>N là trung điểm AF
Mà I là trung điểm BF(gt) => NI là đường trung bình của tam giác FAB
=>NI//AB,NI=1/2AB .Mà AB//CD(ABCD là hình chữ nhật) =>NI//CD hay NI//MC(M thuộc CD) (1)
Vì NI=1/2AB(cmt), AB=CD(ABCD là hcn) => NI=1/2CD
Lại có: M là trung điểm CD(gt) => MC=MD=1/2CD =>NI=MC (2)
Từ (1) và (2) => CINM là hình bình hành
b)Vì NI//CD (cmt), CD vuông góc với BC(ABCD là hình bình hành)
=>NI vuông góc với BC =>NI là đường cao trong tam giác NBC (3)
Vì góc BNM=90 độ(gt) =>BN vuông góc với NM
Lại có :NM//IC(CINM là hình bình hành) =>CI vuông góc với BN
=>CI là đường cao trong tam giác BNC (4)
Từ (3) và (4) =>I là trực tâm trong tam giác BNC =>BI vuông góc với AC hay BF vuông góc với AC
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD. Gọi M là trung điểm của CD, N là một điểm trên đường chéo AC sao cho \(\widehat{BNM}\)=90o. Gọi F là điểm đối xứng của A qua N, I là trung điểm của BF. CMR
a) BF \(\perp\)AC
Có DAB + ABC = 180
Có DAC + CAB = 90 và CBF + FBA = 90
Từ 2 điều trên suy ra FBA + FAB = 90
Xét tam giác ABF có FBA + FAB = 90 (cm trên)
và FBA + FAB + AFB = 180 (3 góc tam giác)
Từ đó suy ra được AFB = 90.
Từ đó biết được đpcm
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hình chữ nhật ABCD có O là giao điểm hai đường chéo AC và BD. Gọi M là trung điểm của OA, N là điểm đối xứng với điểm B qua điểm M.a) Chứng minh tứ giác OMND là hình thang.b) Chứng minh tứ giác AODN là hình thoi.c) Từ N vẽ NE vuông góc với CD (E thuộc CD). Gọi F là giao điểm của AD và ON. Tứ giác DENF là hình gì ?Vì sao ?
Đọc tiếp
Cho hình chữ nhật ABCD có O là giao điểm hai đường chéo AC và BD. Gọi M là trung điểm của OA, N là điểm đối xứng với điểm B qua điểm M.
a) Chứng minh tứ giác OMND là hình thang.
b) Chứng minh tứ giác AODN là hình thoi.
c) Từ N vẽ NE vuông góc với CD (E thuộc CD). Gọi F
là giao điểm của AD và ON. Tứ giác DENF là hình gì ?
Vì sao ?
Cho hình chữ nhật ABCD. Điểm M nằm trên đường chéo AC. gọi N là điểm đối xứng của D qua M, kẻ NH vuông góc với AB và NK vuông góc với BC . Chứng minh 3 điểm M,H,K thẳng hàng