nêu các đỉnh kề, đỉnh đối, cạnh kề, cạnh đối, góc đối, đường chéo của đa giác trên
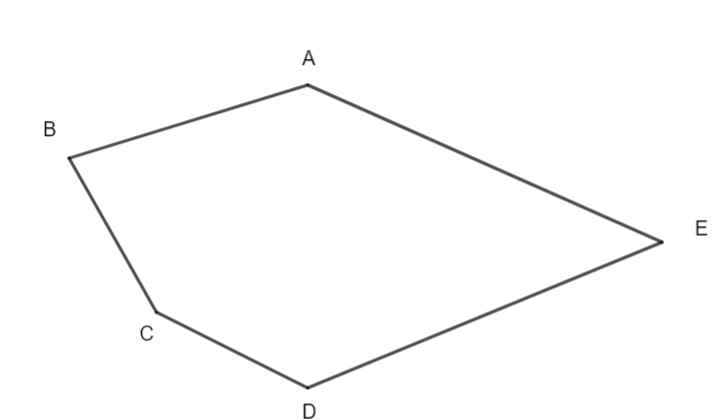
nêu các đỉnh kề, đỉnh đối, cạnh kề, cạnh đối, góc đối, đường chéo của đa giác trên

Quan sát tứ giác ABCD ở hình 3 rồi điền vào chỗ trống:
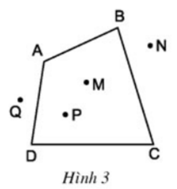
a) Hai đỉnh kề nhau: A và B, …
Hai đỉnh đối nhau: A và C, …
b) Đường chéo (đoạn thẳng nối hai đỉnh đối nhau): AC, …
c) Hai cạnh kề nhau: AB và BC, …
Hai cạnh đối nhau: AB và CD, …
d) Góc: ∠A , …
Hai góc đối nhau: ∠A và ∠C , …
e) Điểm nằm trong tứ giác (điểm trong của tứ giác): M, …
Điểm nằm ngoài tứ giác (điểm ngoài của tứ giác): N, …
a) Hai đỉnh kề nhau: A và B, B và C, C và D, D và A
Hai đỉnh đối nhau: A và C, B và D
b) Đường chéo (đoạn thẳng nối hai đỉnh đối nhau): AC, BD
c) Hai cạnh kề nhau: AB và BC, BC và CD, CD và DA, DA và AB
Hai cạnh đối nhau: AB và CD, AD và BC
d) Góc: ∠A , ∠B , ∠C , ∠D
Hai góc đối nhau: ∠A và ∠C , ∠B và ∠D
e) Điểm nằm trong tứ giác (điểm trong của tứ giác): M, P
Điểm nằm ngoài tứ giác (điểm ngoài của tứ giác): N, Q
Trên bản đồ, tứ giác \(BDNQ\) với các đỉnh là các thành phố Buôn Ma Thuột, Đà Lạt, Nha Trang, Quy Nhơn.
a) Tìm các cạnh kề và cạnh đối diện của cạnh \(BD\).
b) Tìm các đường chéo của tứ giác
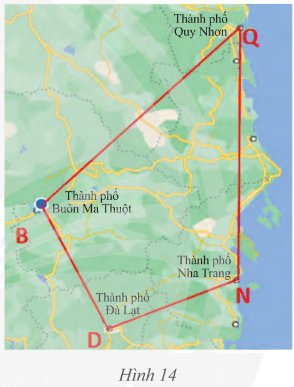
a) Các cạnh kề của \(BD\) là: \(BQ\), \(DN\)
Cạnh đối của cạnh \(BD\) là: \(NQ\)
b) Các đường chéo của tứ giác là: \(BN;\;DQ\)
Hai đường thẳng cắt nhau tạo nên 4 góc (không tính góc bẹt)
(A) đối đỉnh.
(B) đôi một đối đỉnh.
(C) đôi một không kề nhau đối đỉnh.
(D) đôi một chung đỉnh và không chung cạnh đối đỉnh.
Hai đường thẳng cắt nhau tạo nên 4 góc(không tính góc bẹt)
A.đối đỉnh
B.đôi một đối đỉnh
C.đôi một không kề nhau đối đỉnh
D.đôi một chung đỉnh và không chung cạnh đối đỉnh
Quan sát đa giác ABCDEG ở hình 119 rồi điền vào chỗ trống trong các câu sau:
Các đỉnh là các điểm: A, B, …
Các đỉnh kề nhau là: A và B, hoặc B và C, hoặc …
Các cạnh là các đoạn thẳng: AB, BC, …
Các đường chéo là các đoạn thẳng nối hai đỉnh không kề nhau: AC, CG, …
Các góc là: ∠A , ∠B , …
Các điểm nằm trong đa giác (các điểm trong của đa giác) là: M, N, …
Các điểm nằm ngoài đa giác (các điểm ngoài của đa giác) là: Q, …
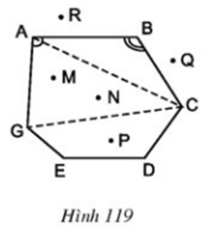
Các đỉnh là các điểm: A, B, C, D, E, G
Các đỉnh kề nhau là: A và B, hoặc B và C, hoặc C và D, hoặc D và E, hoặc E và G, hoặc G và A
Các cạnh là các đoạn thẳng: AB, BC, CD, DE, EG, GA
Các đường chéo là các đoạn thẳng nối hai đỉnh không kề nhau: AC, CG, AD, AE, BG, BE, BD, CE, DG
Các góc là: ∠A , ∠B , ∠C , ∠D , ∠E , ∠G
Các điểm nằm trong đa giác (các điểm trong của đa giác) là: M, N, P
Các điểm nằm ngoài đa giác (các điểm ngoài của đa giác) là: Q, R
Hai đường thẳng cắt nhau tạo nên 4 góc ( không tính góc bẹt)
(A) đối đỉnh
(B) đôi một đối đỉnh
(C) đôi một không kề nhau đối đỉnh
(D) đôi một chung đỉnh và không chung cạnh đối đỉnh
Hãy chọn phương án đúng ?
A) cho góc mOn . Vẽ góc nOt kề bù với góc mOn . Vẽ góc mOz kề bù với góc mOn . Khiu đó mOn và tOz có phải là hai góc đối đỉnh ko?
b)Cho góc hBk. vẽ Bm là tia phân giác của góc hBk . vẽ Bm' là tia đối của tia Bm. Vẽ góc kBj kề bù với góc hBk. khi đó các góc m'Bj và hBm có phải là hai góc đối đỉnh ko
c)cho góc xOy vẽ góc yOz kề bù với góc xOy vẽ gos xOt kề bù với góc xOy. Vẽ Om kề bù với góc zOy vẽ Om là tia phân giác của góc tOxkhi đó zOn và xOm có phải là 2 góc đối đỉnh ko
Ta có:
\(\widehat{mOz}\) kề bù với \(\widehat{mOn}\)
\(\widehat{nOt}\) kề bù với \(\widehat{mOn}\)
\(\Rightarrow\) \(\widehat{mOz}\) và \(\widehat{nOt}\) đối đỉnh
a) Cho góc mOn. Vẽ góc nOt kề bù vs góc mOn. Vẽ góc mOz kề bù vs góc mOn. Khi đó mOn và tOz có phải là 2 góc đối đỉnh ko?
b) Cho góc hBk. Vẽ Bm là tia phân giác của góc hBk. Vẽ Bm' là tia đối của tia Bm. Vẽ góc kBj kề bù vs góc hBk. Khi đó các góc m'Bj và hBm có phải là hai góc đối đỉnh ko?
c) Cho góc xOy. Vẽ góc yOz kề bù vs góc xOy. Vẽ góc xOt kề bù vs góc xOy. Vẽ On là tia phân giác của góc zOy. Vẽ Om là tia phân giác của góc tOx. Khi đó zOn và xOm có fai là 2 góc đối đỉnh ko?
a)
Có vì :
+) mOn kề bù với góc mOz nên On và Oz đối nhau (1)
+) mOn kề bù với nOt nên Om đối Ot (2)
Vì Om đố Ot; On dối Oz nên 2 gốc nOm và tOz dối đỉnh (đpcm)
Tự vẽ hình.
a) Ta thấy: Góc nOt kề bù vs góc mOn, góc mOz kề bù vs góc mOn
=> Góc nOt = Góc mOz. (1)
Góc nOt + Góc mOn = 180 độ (kề bù) (2)
Góc mOz + Góc tOz = 180 độ ( kề bù) (3)
Từ (1) ; (2) ; (3) suy ra Góc mOn = Góc zOt
=> mOt cắt zOn tại O
Vậy: mOn và tOz là 2 góc đối đỉnh
b,c tương tự