Cho ΔABC có AB=5,AC=12,BC=13.Trung tuyến AI
a.Tính AI
b.Hạ IH vuông góc với AB,IK vuông góc với AC.Chứng minh tứ giác AHIK là hình chữ nhật
c.Lấy điểm D đối xứng với I qua điểm H.Chứng minh tứ giác AMBI là hình thoi
Những câu hỏi liên quan
ΔABC vuông tại A,Có I là trung điểm Bc.
A)Cho Ab=6cm ; AC=8cm.Tính AI
B) Từ I kẻ IH ⊥ AB ; IK ⊥ AC.Chứng minh tứ giác AHIK là hình chữ nhật.
C)Vẽ E đ/x I qua K. Chứng minh tứ giác AICE là hình thoi
D) Tính diện tích ΔABC
Chỉ em với ạ huhuhu
a: AI=5cm
b: Xét tứ giác AHIK có
\(\widehat{AHI}=\widehat{AKI}=\widehat{KAH}=90^0\)
Do đó: AHIK là hình chữ nhật
Đúng 0
Bình luận (0)
ΔABC vuông tại A,Có I là trung điểm Bc.
A)Cho Ab=6cm ; AC=8cm.Tính AI
B) Từ I kẻ IH ⊥ AB ; IK ⊥ AC.Chứng minh tứ giác AHIK là hình chữ nhật.
C)Vẽ E đ/x I qua K. Chứng minh tứ giác AICE là hình thoi
D) Tính diện tích ΔABC
a: AI=5cm
b: Xét tứ giác AHIK có
\(\widehat{AHI}=\widehat{AKI}=\widehat{KAH}=90^0\)
Do đó: AHIK là hình chữ nhật
Đúng 0
Bình luận (0)
tam giác ABC vuông tại A. I là trung điểm BC. Vẽ IH vuông góc với AB tại H, IK vuông góc AC tại K.
a) chứng minh tứ giác AHYK là Hình chữ nhật
b) gọi N là trung điểm đối xứng với I qua H. Chứng minh tứ giác ANBI là Hình bình hành
a: Xét tứ giác AHIK có
\(\widehat{AHI}=\widehat{AKI}=\widehat{KAH}=90^0\)
Do đó: AHIK là hình chữ nhật
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A (AB AC).Gọi I là trung điểm của cạnh BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AC tại N.a) Chứng minh tứ giác AMIN là hình chữ nhật.b) Gọi D là điểm đối xứng của I qua N. Chứng minh tứ giác ACID là hình thoi.c) Cho AC 20cm, BC 25cm.Tính diện tích ΔABCd) Đường thẳng BN cắt cạnh DC tại K. Chứng minh:
D
K
D
C
1
3
Đọc tiếp
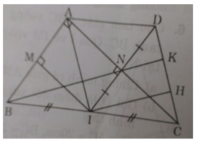
Cho tam giác ABC vuông tại A (AB < AC).Gọi I là trung điểm của cạnh BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AC tại N.
a) Chứng minh tứ giác AMIN là hình chữ nhật.
b) Gọi D là điểm đối xứng của I qua N. Chứng minh tứ giác ACID là hình thoi.
c) Cho AC = 20cm, BC = 25cm.Tính diện tích ΔABC
d) Đường thẳng BN cắt cạnh DC tại K. Chứng minh: D K D C = 1 3
a) Xét tứ giác AMIN có:
∠(MAN) = ∠(ANI) = ∠(IMA) = 90o
⇒ Tứ giác AMIN là hình chữ nhật (có 3 góc vuông).
b) ΔABC vuông có AI là trung tuyến nên AI = IC = BC/2
do đó ΔAIC cân có đường cao IN đồng thời là đường trung tuyến
⇒ NA = NC.
Mặt khác ND = NI (t/c đối xứng) nên ADCI là hình bình hành
Lại có AC ⊥ ID (gt). Do đó ADCI là hình thoi.
c) Ta có: AB2 = BC2 – AC2 (định lí Py-ta-go)
= 252 – 202 ⇒ AB = √225 = 15 (cm)
Vậy SABC = (1/2).AB.AC = (1/2).15.20 = 150 (cm2)
d) Kẻ IH // BK ta có IH là đường trung bình của ΔBKC
⇒ H là trung điểm của CK hay KH = HC (1)
Xét ΔDIH có N là trung điểm của DI, NK // IH (BK // IH)
Do đó K là trung điểm của DH hay DK = KH (2)
Từ (1) và (2) ⇒ DK = KH = HC ⇒ DK/DC= 1/3.
Đúng 1
Bình luận (0)
Cho tam giác ABD vuông tại A, lấy I là trung điểm của BC, kẻ IH vuông góc với AB tại H và IK vuông góc với AC tại K. Gọi E là điểm đối xứng với I qua H.
a) Chứng minh AHIK là hình chữ nhật.
b) Chứng minh AIBE là hình thoi
c) Tìm điều kiện của tam giác ABC để AIBE là hình vuông.
a: Xét tứ giác AHIK có
\(\widehat{AHI}=\widehat{AKI}=\widehat{KAH}=90^0\)
Do đó: AHIK là hình chữ nhật
b: Xét ΔABC có
I là trung điểm của BC
IH//AC
Do đó: H là trung điểm của AB
Xét tứ giác AIBE có
H là trung điểm của AB
H là trung điểm của IE
Do đó: AIBE là hình bình hành
mà IA=IB
nên AIBE là hình thoi
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, trung tuyến AM. Kẻ MD vuông góc với AB tại D; ME vuông góc với AC tại E.
a) Tứ giác ADME là hình gì? Vì sao?
b) Gọi I là điểm đối xứng với M qua D. Chứng minh tứ giác AMBI là hình thoi.
c) Tìm điều kiện của tam giác ABC để tứ giác AMBI là hình vuông.
d) Vẽ đường cao AH của tam giác ABC, kẻ HP vuông góc với AB tại P, HQ vuông góc với AC tại
Q. Chứng minh PQ vuông góc với AM.
Giúp mình câu d nhé!
Đọc tiếp
Cho tam giác ABC vuông tại A, trung tuyến AM. Kẻ MD vuông góc với AB tại D; ME vuông góc với AC tại E.
a) Tứ giác ADME là hình gì? Vì sao?
b) Gọi I là điểm đối xứng với M qua D. Chứng minh tứ giác AMBI là hình thoi.
c) Tìm điều kiện của tam giác ABC để tứ giác AMBI là hình vuông.
d) Vẽ đường cao AH của tam giác ABC, kẻ HP vuông góc với AB tại P, HQ vuông góc với AC tại
Q. Chứng minh PQ vuông góc với AM.
Giúp mình câu d nhé!
Bài 1: Cho tam giác ABC vuông tại A. Vẽ I,K lần lượt là trung điểm của AB,BC. Gọi D là điểm đối xứng của A qua K.a. Chứng minh tứ giác ABDC là hình chữ nhật.b. Gọi E là điểm đối xứng của K qua I. Chứng minh tứ giác AKBE là hình thoi.c. Chứng minh tứ giác AEKC là hình bình hành.d. Tìm điều kiện để hình thoi AKBE là hình vuông.Bài 2: Cho tam gaics ABC vuông tại A, đường cao AH, trung tuyến AM. Gọi D là trung điểm AB, lấy điểm E đối xứng với M qua D.a. Chứng minh: M và E đối xứng nhau qua AB.b. Chứ...
Đọc tiếp
Bài 1: Cho tam giác ABC vuông tại A. Vẽ I,K lần lượt là trung điểm của AB,BC. Gọi D là điểm đối xứng của A qua K.
a. Chứng minh tứ giác ABDC là hình chữ nhật.
b. Gọi E là điểm đối xứng của K qua I. Chứng minh tứ giác AKBE là hình thoi.
c. Chứng minh tứ giác AEKC là hình bình hành.
d. Tìm điều kiện để hình thoi AKBE là hình vuông.
Bài 2: Cho tam gaics ABC vuông tại A, đường cao AH, trung tuyến AM. Gọi D là trung điểm AB, lấy điểm E đối xứng với M qua D.
a. Chứng minh: M và E đối xứng nhau qua AB.
b. Chứng minh: AMBE là hình thoi.
c. Kẻ HK vuông góc với AB tại K, HI vuông góc với AC tại I. Chứng minh IK vuông góc với AM
Bài 3: Cho tam giác ABC có ba góc nhọn, trực tâm H. Đường thẳng vuông góc với AB kẻ từ B cắt từ đường thẳng vuông góc từ AC kẻ từ C tại D.
a. Chứng minh tứ giác BHCD là hình bình hành.
b. Gọi M là trung điểm BC, O là trung điểm AD. Chứng minh 2OM = AH
a)Ta có
BK=KC (GT)
AK=KD( Đối xứng)
suy ra tứ giác ABDC là hình bình hành (1)
mà góc A = 90 độ (2)
từ 1 và 2 suy ra tứ giác ABDC là hình chữ nhật
b) ta có
BI=IA
EI=IK
suy ra tứ giác AKBE là hình bình hành (1)
ta lại có
BC=AD ( tứ giác ABDC là hình chữ nhật)
mà BK=KC
AK=KD
suy ra BK=AK (2)
Từ 1 và 2 suy ra tứ giác AKBE là hình thoi
c) ta có
BI=IA
BK=KC
suy ra IK là đường trung bình
suy ra IK//AC
IK=1/2AC
mà IK=1/2EK
Suy ra EK//AC
EK=AC
Suy ra tứ giác AKBE là hình bình hành
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có đường trung tuyến AD. Kẻ DH vuông góc với AB (H thuộc AB), DE vuông góc với AC (E thuộc AC)
A) Chứng minh tứ giác AHDE là hình chữ nhật?
B) Lấy điểm M đối xứng với điểm D qua điểm E. Chứng minh tứ giác ADCM là hình bình hành?
Cho tam giác ABC vuông tại A có đường trung tuyến AD. Kẻ DH vuông góc với AB (H thuộc AB), DE vuông góc với AC (E thuộc AC)
A) Chứng minh tứ giác AHDE là hình chữ nhật?
B) Lấy điểm M đối xứng với điểm D qua điểm E. Chứng minh tứ giác ADCM là hình bình hành?
Cho minh xin cau tra loi som nhat co the nhe!