
Những câu hỏi liên quan
Tìm các tam giác bằng nhau ở hình dưới (không xét tam giác mà các cạnh chưa được kẻ)
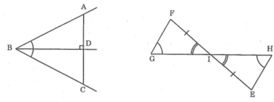
+ ΔABD = ΔCBD (g.c.g) vì:
∠ABD = ∠CBD (gt)
BD chung
∠ADB = ∠BDC (= 90o)
+ Ta có: ∠FGI = ∠IHE ( giả thiết). Mà hai góc này ở vị trí so le trong nên: FG // HE
⇒ ∠GFI = ∠IEH ( hai góc so le trong).
*) Khi đó: ΔGIF = ΔHIE (g.c.g) vì:
∠GFI = ∠IEH ( chứng minh trên)
FI = IE ( giả thiết)
∠GIF = ∠EIH (hai góc đối đỉnh)
Đúng 0
Bình luận (0)
Tìm các tam giác bằng nhau trên hình 55 (sách bài taptoan lớp 7 trang 144)không xét các tam giác mà các cạnh chưa được kể.
Trên hình bên có một số tam giác bằng nhau. Hãy quan sát rồi phát hiện các tam giác bằng nhau trong hình vẽ (không xét các tam giác mà các cạnh chưa được kẻ), sau đó kiểm tra lại bằng cách đo.
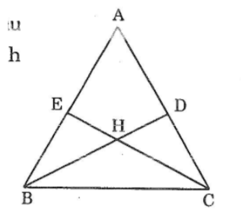
Có ba cặp tam giác bằng nhau:
ΔABD=ΔACE
ΔBEC=ΔCDB
ΔBEH=ΔCDH
Đúng 0
Bình luận (0)
Tìm các tam giác bằng nhau trên hình 55 (không xét các tam giác mà các cạnh chưa được kẻ)
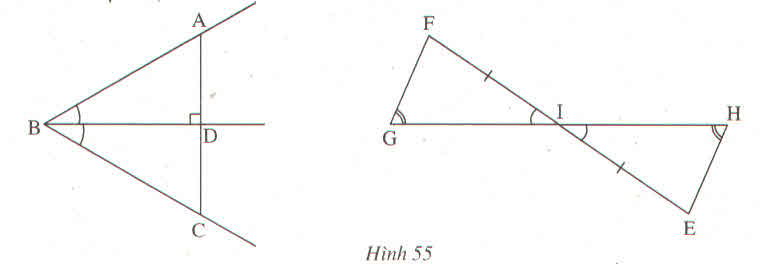
-Xét tam giác vuông BDA và tam giác vuông BDC có:
ABD = CBD
BD: cạnh chung
=> tam giác BDA = tam giác BDC
-Ta có: góc G = góc H
góc FIG = góc EIH
Mà F + G + FIG = E + H + EIH = 1800
=> góc F = góc E
Xét tam giác IFG và tam giác IEH có:
IF = IE (gt)
FIG = EIH (gt)
góc F = góc E (cmt)
=> tam giác IFG = tam giác IEH
Đúng 0
Bình luận (0)
Trên hình 51, có một số tam giác bằng nhau. Hãy quan sát rồi phát hiện các tam giác bằng nhau trong hình vẽ (không xét các tam giác mà các cạnh chưa kẻ) sau đó kiểm tra lại bằng cách đo ?

Các tam giác = nhau là :
\(\Delta ABD\) và \(\Delta BDC\)
\(\Delta BEH\) và \(\Delta CDH\)
\(\Delta AEC\) và \(\Delta BEC\)
Tick minh ha
Đúng 0
Bình luận (0)
Cho tam giác ABC, E là điểm chính giữa cạnh BC. Trên cạch AC lấy điểm F sao cho AF = 2xFC. Đoạn thẳng AE cắt đoạn thẳng BF ở O. Nối O với C
Hãy kể tên các tam giác có trong hìnhHãy tìm trên hình vẽ các tam giác có diện tích bằng nhau. Giải thích tại sao?Cho biết diện tích tam giác OEB là 6cm2. Tính diện tích tam giác ABC và diện tích tứ giác OECF. Từ đó tính tỉ số OF/OB?
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD, hai đường chéo AC và BD cắt nhau tại O. Xét các tam giác có đỉnh lấy trong số các điểm A, B, C, O, hãy chỉ ra các tam giác có diện tích bằng nhau và giải thích vì sao.
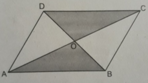
Xem hình bs.52.
- Các tam giác ADB, ACB, DAC, DBC có diện tích bằng nhau vì cùng bằng nửa diện tích hình bình hành đã cho.
- Các tam giác OAD, OCB, ODC, OBA có diện tích bằng nhau vì cùng bằng một phần tư diện tích hình bình hành đã cho.
Đúng 0
Bình luận (0)
Tìm trong các hình 63, 64 các tam giác bằng nhau (các cạnh bằng nhau được đánh dấu bởi những kí hiệu giống nhau). Kể tên các đỉnh tương ứng của các tam giác bằng nhau đó. Viết kí hiệu về sự bằng nhau của các tam giác đó.
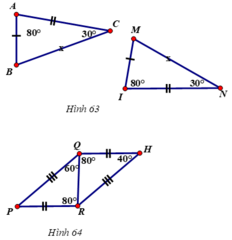
- Xem hình 63)
Ta có:
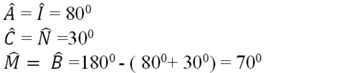
Và AB = MI; AC = IN; BC = MN
Nên ΔABC = ΔIMN
QUẢNG CÁO- Xem hình 64)
ΔPQR có:
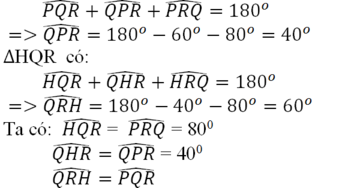
Và QH = RP, HR = PQ, QR cạnh chung
Nên ΔHQR = ΔPRQ
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD, hai đường chéo AC và BD cắt nhau tại O. Xét các tam giác có đỉnh lấy trong số các điểm A, B, C, D, O. Hãy chỉ ra các tam giác có diện tích bằng nhau và giải thích vì sao ?
Ta có:
* SADB=SACB=SDAC=SDBC ( cùng bằng \(\dfrac{1}{2}.S_{hbh}\) )
* SOAD=SOCB=SODC=SOBA (cùng bằng \(\dfrac{1}{4}.S_{hbh}\))
Đúng 0
Bình luận (0)















