
Những câu hỏi liên quan
cho a,b,c,d là các số nguyên thỏa mãn :a^5+b^5=4(c^5+d^5)
CMR:a+b+c+d chia hết cho 5
a^5+b^5=4.(c^5-+d^5)
<=> a^5+b^5+c^5+d^5 = 5.(c^5+d^5) chia hết cho 5
Xét : a^5-a = a(a-2).(a+2).(a-1).(a+1)+5.a.(a-1).(a+1) chia hết cho 5
Tương tự : b^5-b ; c^5-c ; d^5-d đều chia hết cho 5
=> a^5+b^5+c^5+d^5-(a+b+c+d) chia hết cho 5
Mà a^5+b^5+c^5+d^5 chia hết cho 5
=> a+b+c+d chia hết cho 5
Tk mk nha
Đúng 0
Bình luận (0)
Cho a;b;c;d là các số nguyên tố > 2 thỏa mãn a^5+b^5+c^5+d^5 chia hết cho 40.Chứng minh a+b+c+d chia hết cho 40
1)cho D=5+5^2+5^3+5^4+5^5+5^6+...+5^2015+5^2016
a) cmr D chia hết cho 216
b) tìm số tự nhiên x để : 4.D+5=5^x
Một câu hỏi hiếm thấy :3
Xem thêm câu trả lời
cho a^5+b^5=2014(c^5+d^5)
chứng minh rằng a+b+c+d chia hết cho 5
cho a,b,c,d le . c/m a5+b5+c5+d5chia hết cho 240 <=>a+b+c+d chia hết cho 240
Đầu tiên chứng minh. Với mọi số n lẻ thì: \(n^5-n⋮240\)
Vì n lẻ nên ta chứng minh: \(A=\left(2k+1\right)^5-\left(2k+1\right)⋮240\)
Ta có:
\(\left(2k+1\right)^5-\left(2k+1\right)=8k\left(k+1\right)\left(2k+1\right)\left(2k^2+2k+1\right)\)
Chứng minh nó chia hết cho 16.
Vì \(k\left(k+1\right)⋮2\)
\(8k\left(k+1\right)\left(2k+1\right)\left(2k^2+2k+1\right)⋮16\)
Chứng minh nó chia hết cho 3:
Với \(k=3x\) thì \(A⋮3\)
Với \(k=3x+1\) thì \(2k+1=2\left(3x+1\right)+1=6x+3⋮3\)
Với \(k=3x+2\)thì \(k+1=3x+2+1=3x+3⋮3\)
\(\Rightarrow A⋮3\)
Chứng minh tương tự ta có được \(A⋮5\)
Vậy \(A⋮\left(16.3.5=240\right)\)
Quay lại bài toán ta có
\(a^5+b^5+c^5+d^5-a-b-c-d\)
\(=\left(a^5-a\right)+\left(b^5-b\right)+\left(c^5-c\right)+\left(d^5-d\right)⋮240\)
Từ đây ta có ĐPCM
Đúng 0
Bình luận (0)
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
Đúng 0
Bình luận (0)
Cho a,b,c,d là các số nguyên thỏa mãn a+b+c+d=2016 .Chúng minh rằng a^5+b^5+c^5+d^5 chia hết cho 6
Ta có a^5-a luôn chia hết cho 6
suy ra a^5+...+d^5 -2016 chia hết cho 6
dpcm
Cho tỉ lệ thức a/b =c/d (b+d khác 0) a) 5a^5+c^5/5b^5+d^5 =(a+c)^5/(b+d) ^5
\(\dfrac{a}{b}=\dfrac{c}{d}\rightarrow\dfrac{5a^5}{5b^5}=\dfrac{c^5}{d^5}=\dfrac{5a^5+c^5}{5b^5+d^5}\)
\(\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{a+c}{b+d}\)
\(\dfrac{a^5}{b^5}=\dfrac{c^5}{d^5}=\dfrac{\left(a+c\right)^5}{\left(b+d\right)^5}\)
nên ta có
\(\dfrac{5a^5+c^5}{5b^5+d^5}=\dfrac{\left(a+c\right)^5}{\left(b+d\right)^5}\)
Đúng 0
Bình luận (1)
Cho 193(a^5+b^5)=479c^5+d^5)(a,b,c,d là những số lẻ)Chứng minh rằng: a+b+c+d chia hết cho 240
Cho hàm số:Khoảng cách d giữa hai điểm cực trị của đồ thị hàm số là:A. d 2
5
B. d
5
/4C. d
5
D.
5
/2
Đọc tiếp
Cho hàm số:
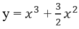
Khoảng cách d giữa hai điểm cực trị của đồ thị hàm số là:
A. d = 2 5 B. d = 5 /4
C. d = 5 D. 5 /2
Đáp án: D.
y' = 3 x 2 + 3x = 3x(x + 1) = 0
⇔ 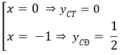
Vậy khoảng cách giữa hai điểm cực trị là:
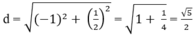
Đúng 0
Bình luận (0)
Cho a,b,c,d là các số nguyên tố >2 và a^5+b^5+c^5+d^5 chia hết cho 40
CHỨNG MINH:a+b+c+d chia hết cho 40
giúp mik nha mik tikkk
Xét : a^5-a = a.(a^4-1) = a.(a^2-1).(a^2+1) = (a-1).a.(a+1).(a^2-4+5)
= (a-2).(a-1).a.(a+1).(a+2)+5.(a-1).a.(a+1)
Ta thấy a-2;a-1;a;a+1;a+2 là 5 số tự nhiên liên tiếp nên có 1 số chia hết cho 2 ; 1 số khác chia hết cho 4 ; 1 số chia hết cho 5
=> (a-2).(a-1).a.(a+1).(a+2) chia hết cho 2.4.5 = 40 (1)
Lại có : p là số nguyên tố > 2 => p lẻ => p = 2k+1 ( k thuộc N sao )
=> (p-1).(p+1) = 2k.(2k+2) = 4.k.(k+1)
Vì k;k+1 là 2 số tự nhiên liên tiếp nên có 1 số chia hết cho 2
=> (p-1).(p+1) chia hết cho 8
=> 5.(p-1).p.(p+1) chia hết cho 5.8=40 (2)
Từ (1) và (2) => a^5-a chia hết cho 40
Tương tự : b^5-b ; c^5-c ; d^5-d đều chia hết cho 40
=> (a^5+b^5+c^5+d^5)-(a+b+c+d) chia hết cho 40
Mà a^5+b^5+c^5+d^5 chia hết cho 40 => a+b+c+d chia hết cho 40
Tk mk nha
Đúng 0
Bình luận (0)





















