
Những câu hỏi liên quan
1.Cho tam giác ABC các tia phân giác của góc B và góc C cắt nhau ở O..Gọi DEF lần lượt là chân đường vuông góc kẻ từ điểm O đến BC,CA,AB(D thuộc BC,E thuộc AC,F thuộc AB) tia Ao cắt BC ở M.CMR a,ODOEOF b,Góc MOCgóc DOB 2.Cho tam giác abc có góc A bằng 120 độ.Các tia phân giác của góc A và góc C cắt nhau ở O,cắt các cạnh BC và AB lần lượt ở D và E.Đường phân giác góc ngoài tại đỉnh B của tam giác ABC cắt đường thẳng AC ở F.CM a,BO vuông góc BF b,góc BDFgóc ADF c,3 điểm DEF thẳng hàng 3.CMR 1 tam...
Đọc tiếp
1.Cho tam giác ABC các tia phân giác của góc B và góc C cắt nhau ở O..Gọi DEF lần lượt là chân đường vuông góc kẻ từ điểm O đến BC,CA,AB(D thuộc BC,E thuộc AC,F thuộc AB) tia Ao cắt BC ở M.CMR a,OD=OE=OF b,Góc MOC=góc DOB 2.Cho tam giác abc có góc A bằng 120 độ.Các tia phân giác của góc A và góc C cắt nhau ở O,cắt các cạnh BC và AB lần lượt ở D và E.Đường phân giác góc ngoài tại đỉnh B của tam giác ABC cắt đường thẳng AC ở F.CM a,BO vuông góc BF b,góc BDF=góc ADF c,3 điểm DEF thẳng hàng 3.CMR 1 tam giác có 1 trung tuyến đồng thời là phân giác thì tam giác đó là tam giác cân CẦN 1 AI ĐÓ GIẢI HỘ Ạ!!MAI PHẢI NỘP RỒI AI LÀM DÙM VỚI Ạ!!
Cho tam giác ABC góc A bằng 120 độ các tia phân giác của góc A và C cắt nhau ở O, cắt các cạnh BC và AB lần lượt ở D và E. Đường phân giác góc ngoài tại đỉnh B của tam giác ABC cắt đường thẳng AC tại F. Chứng minh a,BO vuông góc với BF b, góc BDF bằng góc ADF c, 3 điểm D, E, F thẳng hàng
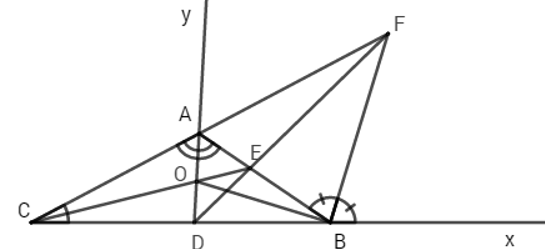
a) Xét \(\Delta ABC\) có tia phân giác \(BAC,ACB\) cắt nhau tại O suy ra O là giao điểm của 3 đường phân giác trong tam giác ABC suy ra BO là phân giác của \(\widehat{CBA}\) (tính chất 3 đường phân giác của tam giác)
\(\Rightarrow DBO=ABO=\dfrac{DBA}{2}\left(1\right)\) ( tính chất tia phân giác )
Lại có BF là phân giác của \(\widehat{ABx\left(gt\right)}\) \(=ABF=FBx\left(2\right)\)
( tính chất của tia phân giác )
Mà \(ABD+ABx=180^o\left(3\right)\left(kềbu\right)\)
Từ \(\left(1\right)\left(2\right)\left(3\right)\Rightarrow OBA+ABF=180^o\div2=90^o\Rightarrow BO\text{⊥ }BF\)
b) Ta có \(FAB+BAC=180^o\)( kề bù ) mà \(BAC=120^o\left(gt\right)\Rightarrow FAB=60^o\)
\(\Rightarrow\text{AD là phân giác của}\widehat{BAC}\) ( dấu hiệu nhận biết tia phân giác )
\(\Rightarrow BAD=CAD=60^o\) ( tính chất tia phân giác )
\(\Rightarrow FAy=CAD=60^o\) ( đối đỉnh ) \(\Rightarrow FAB=FAy=60^o\Rightarrow\) AF là tia phân giác của \(BAy\) ( dấu hiệu nhận biết tia phân giác )
Vậy \(\Delta ABD\) có hai tia phân giác của hai góc ngoài tại đỉnh A và đỉnh B cắt nhau tại F nên suy ra DF là phân giác của \(ADB=BDF=ADF\) ( tính chất tia phân giác )
c) Xét \(\Delta ACD\) có phân giác góc ngoài tại đỉnh A và phân giác trong tại đỉnh C cắt nhau tại E nên suy ra DE cũng là phân giác của \(ADB\Rightarrow\)\(D,E,F\) thẳng hàng
Đúng 6
Bình luận (1)
Bài 1: Cho tam giac ABC, M là trung điểm cua AB. Đường thẳng qua M và song song với BC cắt AC ở I và song song với AB cắt BC ở k. Chứng minh rằng: a) AMIK b) Tam giác AMI bằng tam giác IKC c) AIIC Bài 2: Cho tam giác ABC vuông tại A. Gọi I là trung điểm BC. Trên tia đối của tia IA lấy điểm D sao cho IDIA a) CMR tam giác BID bằng tam giác CIA b) CMR : BD vuông góc với AB c) Qua A kẻ đường thẳng song song với BC cắt đường thẳng BD tại M. C/M tam giác BAM bằng tam giác ABC d) CMR: AB là tia phân gi...
Đọc tiếp
Bài 1: Cho tam giac ABC, M là trung điểm cua AB. Đường thẳng qua M và song song với BC cắt AC ở I và song song với AB cắt BC ở k. Chứng minh rằng: a) AM=IK b) Tam giác AMI bằng tam giác IKC c) AI=IC Bài 2: Cho tam giác ABC vuông tại A. Gọi I là trung điểm BC. Trên tia đối của tia IA lấy điểm D sao cho ID=IA a) CMR tam giác BID bằng tam giác CIA b) CMR : BD vuông góc với AB c) Qua A kẻ đường thẳng song song với BC cắt đường thẳng BD tại M. C/M tam giác BAM bằng tam giác ABC d) CMR: AB là tia phân giác cuả góc DAM Bài 3: Cho tam giác ABC vuông ở A và AB=AC.Gọi K là trung điểm của BC a) C/M: tam giác AKB bằng tam giác AKC b) C/M: AK vuông góc với BC c) từ C vẽ đường vuông góc với BC cắt đường thẳng AB tại E.C/M EK song song với AK Bài 4: Cho tam giác ABC có AB=AC, kẻ BD vuông góc với AC, CE vuông góc với AB(D thuộc AC, E thuộc AB). Gọi O là giao điểm của BD và CE. CMR a) BD= CE b) tam giác OEB bằng tam giác ODC c) AO là tia phân giác cua góc BAC
1. Câu hỏi của 1234567890 - Toán lớp 7 - Học toán với OnlineMath
Bài 1: Cho tam giác ABC, hai đường phân giác BD và CE của tam giác cắt nhau tại O. Tia AO cắt BC tại M. Tam giác ABC phải có điều kiện gì để AM vuông góc với BC.Bài 2: Cho tam giác ABC có góc A 50°. Đường phân giác của góc B và đường phân giác ngoài tại đỉnh C của tam giác cắt nhau tại O. Tính số đo góc BAO.Bài 3: Cho tam giác ABC, các tia phân giác của các góc B và C cắt nhau tại O. Từ A vẽ một đường thẳng vuông góc với OA, cắt các tia BO và CO lần lượt tại M và N. CMR: BM vuông góc với BN, CM...
Đọc tiếp
Bài 1: Cho tam giác ABC, hai đường phân giác BD và CE của tam giác cắt nhau tại O. Tia AO cắt BC tại M. Tam giác ABC phải có điều kiện gì để AM vuông góc với BC.
Bài 2: Cho tam giác ABC có góc A= 50°. Đường phân giác của góc B và đường phân giác ngoài tại đỉnh C của tam giác cắt nhau tại O. Tính số đo góc BAO.
Bài 3: Cho tam giác ABC, các tia phân giác của các góc B và C cắt nhau tại O. Từ A vẽ một đường thẳng vuông góc với OA, cắt các tia BO và CO lần lượt tại M và N. CMR: BM vuông góc với BN, CM vuông góc với CN.
Mọi người giúp mình nhanh nha😙😙😙😙
Câu hỏi của Nguyễn Quang Nam - Toán lớp 8 - Học toán với OnlineMath
Tham khảo bài 3 tại link trên nhé!
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC có AB AC. kẻ AE là tia phân giác của góc BAC ( E thuộc BC). CMR:a) Tam giác ABE tam giác ACEb) AE là đường trung trực của đoạn thằng BC.Bài 2: Cho tam giác ABC, đường cao AH. Trên nửa mặt phảng bờ AC không chứa B, vẽ tam giác ACD sao cho AD BC; CD AB. CMR:a) AB song song với CDb) AH vuông góc với AD.Bài 3: Cho tam giác ABC vuông tại A. Biết tam giác ABC tam giác DEF; tam giác DEF tam giác HIK và AB 2cm; DF 2cm. CMR: Tam giác HIK là tam giác vuông cân.Bài 4: Cho t...
Đọc tiếp
Bài 1: Cho tam giác ABC có AB = AC. kẻ AE là tia phân giác của góc BAC ( E thuộc BC). CMR:
a) Tam giác ABE = tam giác ACE
b) AE là đường trung trực của đoạn thằng BC.
Bài 2: Cho tam giác ABC, đường cao AH. Trên nửa mặt phảng bờ AC không chứa B, vẽ tam giác ACD sao cho AD = BC; CD = AB. CMR:
a) AB song song với CD
b) AH vuông góc với AD.
Bài 3: Cho tam giác ABC vuông tại A. Biết tam giác ABC = tam giác DEF; tam giác DEF = tam giác HIK và AB = 2cm; DF = 2cm. CMR: Tam giác HIK là tam giác vuông cân.
Bài 4: Cho tam giác ABC = tam giác DEF. Biết 2 tia phân giác của góc B và góc C cắt nhau tại O tạo thành góc BOC = 135 độ và góc B = 2 lần góc C. Tính các góc của tam giác DEF.
( bạn tự vẽ hình)
a, xét tam giác ABE và tam giác ACE có:
AE chung
AB=AC (gt)
góc BAE=góc CAE( vì AE là tia phân giác của góc BAC)
=> tam giác ABE=tam giác ACE
b, vì tam giác ABE=tam giác ACE( cmt)=> BE=CE( 2 cạnh tương ứng)(1)
=> góc BEA=góc CEA ( 2 góc tương ứng)
mà 2 góc này kề bù
=> góc BEA=góc CEA= 180 độ : 2= 90 độ
=> AE vuông góc với BC (2)
từ (1) và (2) ta có AE là đường trung trực của BC.
Đúng 0
Bình luận (0)
a, xét tam giác ABE và tam giác ACE có:
AE chung
AB=AC (gt)
góc BAE=góc CAE( vì AE là tia phân giác của góc BAC)
=> tam giác ABE=tam giác ACE
b, vì tam giác ABE=tam giác ACE( cmt)=> BE=CE( 2 cạnh tương ứng)(1)
=> góc BEA=góc CEA ( 2 góc tương ứng)
mà 2 góc này kề bù
=> góc BEA=góc CEA= 180 độ : 2= 90 độ
=> AE vuông góc với BC (2)
từ (1) và (2) ta có AE là đường trung trực của BC.
cho tam giác tại B đường phân giác AD. KẺ BO vuông góc với AD (O thuộc AD). BO cắt AC tại E. CMR
a, tam giac ABO= tam giác AEO
b, tam giác BAE cân
c, AD là đường trung trực của BE
d, kẻ BK vuông góc AC ( K thuộc AC) gọi M là giao điểm của bk và AD. CMR ME//BC
* Nên ghi rõ đề ra nha bạn ( có vài ý là mình bổ sung vào ) *
a) Xét \(\Delta ABO\)và \(\Delta AEO\)ta có:
\(\widehat{A_1}=\widehat{A_2}\)
\(\widehat{AOB}=\widehat{ACE}\left(=90^o\right)\)
\(\text{AD chung}\)
\(\Rightarrow\Delta ABO=\Delta AEO\text{ }\)\(\text{(*)}\)
b) Từ \(\text{(*)}\)\(\Rightarrow AB=AE\)( hai cạnh tương ứng )
\(\Rightarrow\Delta ABE\)là tam giác cân
c) Từ \(\text{(*)}\)\(\Rightarrow OB=OE\)( hai cạnh tương ứng )
Mà \(AD\perp BE\Rightarrow AD\)là đường trung trực của \(BE\)
d) Xét \(\Delta ABE\)ta có:
\(AO\)và \(BK\)là đường cao cắt nhau tại \(M\)
\(\Rightarrow M\)là trực tâm của tam giác
\(\Rightarrow EM\)là đường cao của tam giác
\(\Rightarrow ME\perp AB\)mà \(AB\perp BC\)
\(\Rightarrow ME//BC\)
Cho tam giác ABC vuông tại B, đường phân giác AD ( D thuộc BC ). Kẻ BO vuông góc AD(O thuộc AD),BO cắt AC tại E.C/M rằng
a Tam giác AOB=Tam giác AOE
b Tam giác BAE cân
c AD là đường trung trực của BE
d Kẻ BK vuông góc với AC (K thuộc AC).Gọi M là giao điểm của BK.C/M ME song song với BC
Vẽ hình với
cho tam giác ABC có góc A= 120 độ Các tia phân giác của góc A và góc C cắt ở O, cắ bc và AB lần lượt ở D và E . Đường phân giác các góc ngoài tại đỉnh B của tam giác ABC cắt đường thẳng AC ở F . cm
a, BO vuông góc BE
b, góc BDE = góc ADF
c 3 điểm S,E,F thẳng hàng
mình chọn c k cho mình rồi mình kết bạn
Đúng 0
Bình luận (0)
cho tam giác ABC. các tia phân giác của các góc B và C cắt nhau tại O. kẻ oe, of, og theo thứ tự vuông góc với các cạch AC, AB, BC. tia OA cắt BC tại D. CMR góc BOD=COGcho tam giác ABC. các tia phân giác của các góc B và C cắt nhau tại O. kẻ oe, of, og theo thứ tự vuông góc với các cạch AC, AB, BC. tia OA cắt BC tại D. CMR góc BOD=COG

















