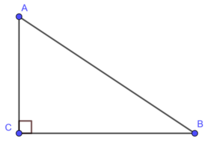
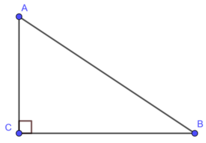
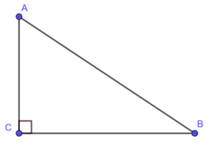
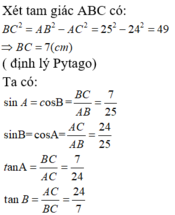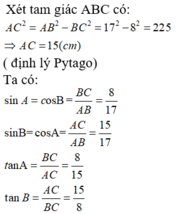Tính sin, cos, tan của các góc A và B của tam giác ABC vuông ở C biết: BC = 1, AC = 2

Những câu hỏi liên quan
Tính sin, cos, tan của các góc A và B của tam giác ABC vuông ở C biết: BC = 21, AC = 20
Tính sin, cos, tan của các góc A và B của tam giác ABC vuông ở C biết: AC = 24, AB = 25
Tính sin, cos, tan của các góc A và B của tam giác ABC vuông ở C biết: BC = 8, AB = 17
BÀI 1 :cho tam giác ABC vuông tại A có AB=4cm BC=6cm. tính tỉ số lượng giác của các góc B và C
BÀI 2 :đơn giản các biểu thức
a)\(A=\cos^2x+\cos^2x.\cot g^2x\)
b)\(sin^2x+\sin^2x.\tan^2x\)
c)\(\dfrac{2cos^2x-1}{\sin x+\cos x}\)
d)\(\dfrac{\cos x}{1+\sin x}+\tan x\)
1. Cho tam giác ABC vuông tại A, đường cao AH, biết AB=4cm,AC=9cm. Tính sin B, sin C
2.Cho tam giác ABC vuông tại A, Cos B= an pha, Cos = 4/5. Tính sin, tan,cos
3. Cho tam giác ABC vuông tại A, đường cao AH, biết AB=6cm, BC= 10cm
a. Tính AC,AH. Tỉ số đồng giác góc B,C
b. Gọi E,F lần lượt là hình chiếu H lên AB,AC. CM :AE.AD=AF.AC
c. Tính S tứ giác AEHF
Bài 1: Biêt sin a = 0,6. Tính cos a, tg a, cotg a?
Bài 2 : biết tg a =2. Tính sin a, cos a, cotg a?
Bài 3: Cho tam giác ABC biết AB = 5, BC = 12, AC= 13
a, Chứng minh rằng tam giác ABC vuông
b, Tính tỉ số lượng giác của góc A và góc C
Bài 1:
\(\cos\alpha=\dfrac{4}{5}\)
\(\tan\alpha=\dfrac{3}{4}\)
\(\cot\alpha=\dfrac{4}{3}\)
Đúng 0
Bình luận (0)
cho tam giác abc có A^=90 độ AB= 6cm và AC = 8cm a/ tính Bc? b/ tính sin B và Tan C? C/ gọi AH là đường cao tam giác ABC , tính cos BAH^,d/ Gọi M là trung điểm Bc từ M kẻ đường thẳng vuông góc với BC cắt AC tại T tính độ dài AT?
a: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay BC=10(cm)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A,AC=5,cot của góc B=2,4.Tính AB,BC.Tính sin,cos,tan,cot của góc C
Cho tam giác ABC vuông tại C, BC = 12cm, AC = 9cm. Tính sin A, cos B, tan A và cot B
Áp dụng định lý Pitago:
\(AB=\sqrt{BC^2+AC^2}=15\left(cm\right)\)
\(sinA=\dfrac{BC}{AB}=\dfrac{12}{15}=\dfrac{4}{5}\)
\(cosB=\dfrac{BC}{AB}=\dfrac{4}{5}\)
\(tanA=\dfrac{BC}{AC}=\dfrac{12}{9}=\dfrac{4}{3}\)
\(cotB=\dfrac{BC}{AC}=\dfrac{4}{3}\)
Đúng 1
Bình luận (0)
Áp dụng định lí Pytago vào ΔABC vuông tại C, ta được:
\(AB^2=CA^2+CB^2\)
\(\Leftrightarrow AB^2=9^2+12^2=225\)
hay AB=15(cm)
Xét ΔABC vuông tại C có
\(\sin\widehat{A}=\dfrac{CB}{AB}=\dfrac{12}{15}=\dfrac{4}{5}\)
\(\cos\widehat{B}=\dfrac{CB}{AB}=\dfrac{12}{15}=\dfrac{4}{5}\)
\(\tan\widehat{A}=\dfrac{CB}{CA}=\dfrac{12}{9}=\dfrac{4}{3}\)
\(\cot\widehat{B}=\dfrac{CB}{CA}=\dfrac{12}{9}=\dfrac{4}{3}\)
Đúng 0
Bình luận (0)