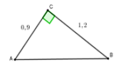
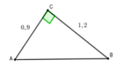
Tam giác ABC vuông tại A, có AC = (1/2).BC. Tính sinB, cosB, tgB, cotgB

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, có AC = 1/2BC. Tính: sinB, cosB, tgB, cotgB
Lời giải:
Đặt \(AC=\frac{BC}{2}=a\) \(\Rightarrow BC=2a\)
Áp dụng định lý Pitago:
\(AB=\sqrt{BC^2-AC^2}=\sqrt{(2a)^2-a^2}=\sqrt{3}a\)
Vậy:
\(\sin B=\frac{AC}{BC}=\frac{a}{2a}=\frac{1}{2}\)
\(\cos B=\frac{AB}{BC}=\frac{\sqrt{3}a}{2a}=\frac{\sqrt{3}}{2}\)
\(\tan B=\frac{AC}{AB}=\frac{a}{\sqrt{3}a}=\frac{1}{\sqrt{3}}\)
\(\cot B=\frac{AB}{AC}=\frac{\sqrt{3}a}{a}=\sqrt{3}\)
Đúng 0
Bình luận (1)
Cho tam giác vuông ở A . Biết sinB = \(\frac{3}{5}\) . Tính cosB , tgB , cotgB
Vì sinB = \(\frac{3}{5}\) , ta có : sin2B + cos2B = 1
nên cos2B = 1 - sin2B = 1 - ( \(\frac{3}{5}\) )2 = 1 - \(\frac{9}{25}\) = \(\frac{16}{25}\)
Vậy cosB = \(\frac{4}{5}\) ( vì cosB > 0 )
Suy ra : tgB = sinB : cosB = \(\frac{3}{5}\) : \(\frac{4}{5}\) = \(\frac{3}{4}\)
cotgB = cosB : sinB = \(\frac{4}{5}\) : \(\frac{3}{5}\) = \(\frac{4}{3}\)
Đúng 0
Bình luận (3)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại C . Hãy tinhs sinA,cosA,tgA,sinB,cosB,tgB,cotgB biết cotgA=1
1.Vẽ tam giác ABC vuông tại A đường cao AH, tính BC,AH,CH,cosB,cosC,sinB,sinC theo trg hợp sau
1,AB=2cm, góc C =45 độ
2,AB=6cm,góc B= 60 độ
2. đề như b1 bỏ cos,sin tính tgB,tgC,cotgB,cotgC
1,AC=4cm,C=45 độ
2,AB=6,C=30 độ
3.đề như b1: 1,CH=75cm,C=30 độ 2, BH=2cm,B =45 độ làm giúp mình với 7h mình phải đi rồi :(((( cảm ơn ạ
mng ơi giúp mình với ạ
mình trả lời hơi muộn :(
1, Theo giả thiết ta có C = 45* nên tam giác ABC là tam giác vuông cân
Suy ra AB = AC = 2 (cm) Mà theo đánh giá của Pitago thì :BC^2 = 8 <=> BC = căn 8
Ta có hệ thức lượng sau : AB.AC=AH.BC <=> 4=căn 8 . AH<=> AH=2/căn2
Lại có hệ thức lượng sau : AC^2=CH.BC<=>4=căn 8 . CH <=> CH=2/căn2
Mặt khác : +)Cos alpha = AB/BC = 2/căn8 = 1/căn2
+)Cos beta = AC/BC = 2/căn8 = 1/căn2
+) Sin alpha = AC/BC = 2/căn8 = 1/căn2
+) Sin beta = AB/BC = 2/căn8 = 1/căn2
Vậy ...
Mấy câu còn lại để từ từ mình làm dần
Cho tam giác ABC vuông tại C có BC = 1,2cm, AC = 0,9cm. Tính các tỉ số lượng giác sinB và cosB.
A. sin B = 0,6; cos B = 0,8
B. sin B = 0,8; cos B = 0,6
C. sin B = 0,4; cos B = 0,8
D. sin B = 0,6; cos B = 0,4
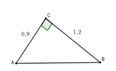
Theo định lý Py-ta-go ta có:
![]()
Xét tam giác ABC vuông tại C có:
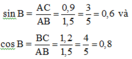
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Tam giác abc vuông tại a, có ac=1/2cb. Tính sinb, cosb, tanb, cotb.
Cho tam giác ABC vuông tại c có BC = 1,2 cm, AC = 0,9 cm . Tính các tỉ số lượng giác sinB; cosB
A. sinB = 0,6 cosB = 0,8
B. sinB = 0,8 cosB = 0,6
C. sinB = 0,4 cosB = 0,8
D. sinB = 0,6 cosB = 0,4
Cho tam giác ABC vuông tại c có BC = 1,2 cm, AC = 0,9 cm . Tính các tỉ số lượng giác sinB; cosB
A. sin B = 0,6; cos B = 0,8
B. sin B = 0,8; cos B = 0,6
C. sin B = 0,4; cos B = 0,8
D. sin B = 0,6; cos B = 0,4
Cho tam giác ABC có đường cao AH( H nằm giữa B và C và AB<AC).
a) Chứng minh AH=BC:(1/tgB+1/tgC).
b) Chứng minh Sabc=1/2CA.CB.sinC.
c) Chứng minh sinB+cosB>1.
d) Gọi E, F lần lượt là hình chiếu H lên AB và AC. Tia FE cắt BC tại D. Chứng minh DE.DF= DB.DC.DH^2.
e) Nếu AH^2= HB.HC. Khi đó chứng minh Tam giác ABC vuông.