Biết 3 số hạng đầu của cấp số cộng là -2;x;6. Tìm số hạng thứ 5 của cấp số cộng đó?
A. 2
B. 18
C. 10
D. 14
Biết 3 số hạng đầu của cấp số cộng là - 2 ; x ; 6 . Tìm số hạng thứ 5 của cấp số cộng đó?
A. 2
B. 18
C. 10
D. 14
Phương pháp
Sử dụng tính chất của cấp số cộng
u k = u k - 1 + u k + 1 2 tìm x
Tính công sai d và sử dụng công thức tìm số hạng thứ n là
u n = u 1 + ( n - 1 ) d
Cách giải:
Áp dụng tính chất các số hạng của cấp số cộng ta có
x = - 2 + 6 2 = 2
Suy ra d = u 2 - u 1 = 4
⇒ u 5 = u 1 + 4 d = 14
Chọn D
Viết 3 số hạng đầu của một cấp số cộng, biết rằng tổng n số hạng đầu tiên của cấp số này là :
\(S_n=4n^2-3n\)
Cho cấp số cộng u n với số hạng đầu u 1 = 2 và số hạng thứ năm u 5 = 14 . Tổng của 10 số hạng đầu của cấp số cộng u n là
A. 232
B. 126
C. 155
D. 187
Ba số phân biệt có tổng 217, là các số hạng liên tiếp của một cấp số nhân, theo thứ tự đó chúng lần lượt là số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng. Biết tổng của n số hạng đầu tiên của cấp số cộng là 820, khi đó n bằng
A. 21
B. 42
C. 20
D. 17
Chọn C
Gọi ba số đó lần lượt là x,y,z
Do ba số là các số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng nên ta có liên hệ: y = x + 7 d , z = x + 42 (với d là công sai của cấp số cộng)
Theo giả thiết ta có: x + y + z = x + x + 7 d + x + 42 d = 3 x + 49 d = 217
Mặt khác do x,y,z là các số hạng liên tiếp của một cấp số nhân nên
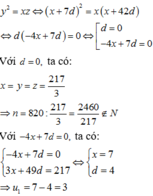
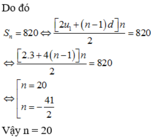
Ba số phân biệt có tổng 217, là các số hạng liên tiếp của một cấp số nhân, theo thứ tự đó chúng lần lượt là số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng. Biết tổng của n số hạng đầu tiên của cấp số cộng là 820, khi đó n bằng
A. 21
B. 42
C.20
D. 17
Viết ba số hạng đầu của một cấp số cộng, biết rằng tổng n số hạng đầu tiên của cấp số này là: S n = 4 n 2 - 3 n
Tìm số hạng đầu của cấp số nhân có bốn số hạng, biết tổng ba số hạng đầu bằng 16 4 9 , đồng thời theo thứ tự, chúng là số hạng thứ nhất, thứ tư và thứ tám của một cấp số cộng.
A. 4
B. 16/9
C. 2/3
D. -1
Chọn A
Gọi u1,u2,u3,u4 là 4 số hạng đầu tiên của cấp số nhân, với công bội q. gọi (vn) là cấp số cộng tương ứng với công sai là d. Theo giả thuyết Ta có:
u 1 + u 2 + u 3 = 16 4 9 u 1 = v 1 u 2 = v 4 = v 1 + 3 d u 3 = v 8 = v 1 + 7 d ⇔ u 1 + u 1 q + u 2 q 2 = 16 4 9 1 u 1 q = u 1 + 3 d 2 u 1 q 2 = u 1 + 7 d 3
Khử d từ (2) và (3) ta thu được:
7 u 1 q = 7 u 1 + 21 d 3 u 1 q 2 = 3 u 1 + 21 d
Lấy vế trừ vế ta thu được
7 u 1 q − 3 u 1 q 2 = 4 u 1 ⇔ u 1 . 3 q 2 − 7 q + 4 = 0 ⇔ u 1 = 0 3 q 2 − 7 q + 4 = 0
Do u 1 ≠ 0 ⇒ q = 1 q = 4 3
Theo định nghĩa cấp số nhận thì q ≠ 1 . Do đó q = 4 3
Thay q = 4 3 vào (1) ta được u 1 = 4
Cho cấp số cộng ( u n ) và gọi S n là tổng n số hạng đầu tiên của nó. Biết S 7 = 77 , S 1 2 = 192 . Tìm số hạng tổng quát u n của cấp số cộng đó
A. u n =5+4n
B. u n =3+2n x
C. u n =2+3n
D. u n =4+5n
Cho u n là cấp số cộng biết u 3 + u 13 = 80. Tổng 15 số hạng đầu của cấp số cộng đó bằng:
A. 800
B. 570
C. 600
D. 630