Cho mặt phẳng (α) có phương trình: 3x + 5y - z - 2 = 0 và đường thẳng d có phương trình: x = 12 + 4 t y = 9 + 3 t z = 1 + t
Viết phương trình mặt phẳng β chứa điểm M và vuông góc với đường thẳng d.
Cho mặt phẳng (α) có phương trình: 3x + 5y - z - 2 = 0 và đường thẳng d có phương trình: x = 12 + 4 t y = 9 + 3 t z = 1 + t
Tìm giao điểm M của đường thẳng d và mặt phẳng α .
M ∈ d ⇒ M(12 + 4t; 9 +3t; 1 + t).
M ∈ α ⇒ 3.(12 + 4t) + 5.(9 + 3t) – (1 + t) – 2 = 0
⇔ 26t + 78 = 0.
⇔ t = -3.
⇒ M(0; 0; -2).
Cho mặt phẳng α : 3x+5y-z-2=0 và đường thẳng d : x = 12 + 4 t y = 9 + 3 t z = 1 + t Gọi M là tọa độ giao điểm của đường thẳng d và mặt phẳng α . Viết phương trình mặt phẳng (P) chứa điểm M và vuông góc với đường thẳng d
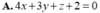
![]()
![]()
![]()
Cho mặt phẳng ( α ) : 3 x + 5 y - z - 2 = 0 và đường thẳng d : x = 12 + 4 t y = 9 + 3 t z = 1 + t . Gọi M là tọa độ giao điểm của đường thẳng d và mặt phẳng (α). Viết phương trình mặt phẳng (P) chứa điểm M và vuông góc với đường thẳng d
A. 4 x + 3 y + z + 2 = 0
B. 4 x - 3 y + z + 2 = 0
C. 4 x - 3 y - z + 2 = 0
D. 4 x + 3 y + z = 0
Chọn A
Tìm tọa độ giao điểm M bằng cách giải hệ. Mặt phẳng (P) cần tìm qua điểm M và nhận vecto chỉ phương của d làm vecto pháp tuyến.
Trong không gian Oxyz, cho mặt phẳng ( α ) : 3 x + y + z = 0 và đường thẳng △ : x - 3 1 = y + 4 - 2 = z - 1 2 . Phương trình của đường thẳng d nằm trong mặt phẳng ( α ) , cắt và vuông góc với đường thẳng △ là
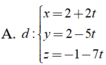
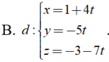
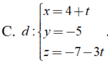
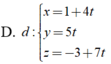
Trong không gian tọa độ Oxyz cho đường thẳng có phương trình x - 1 2 = y + 1 - 1 = z 2 và mặt phẳng α có phương trình x+y-z-2=0. Tính côsin của góc tạo bởi đường thẳng ∆ và mặt phẳng α
![]()
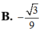
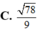
![]()
Trong không gian tọa độ Oxyz cho đường thẳng △ có phương trình x - 1 2 = y + 1 - 1 = z 2 và mặt phẳng ( α ) có phương trình x+y-z-2=0 Tính côsin của góc tạo bởi đường thẳng △ và mặt phẳng ( α )
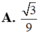
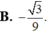
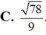
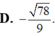
Trong mặt phẳng Oxy cho hình (H) gồm đường thẳng d có phương trình: 3x - 5y + 7 = 0; đường thẳng d’ có phương trình 3x - 5y + 12 = 0. Một tâm đối xứng của (H) là:
A. (1;2)
B. (-4;0)
C. (0;19/10)
D. (19/10;0)
Hai đường thẳng d và d’ song song. Điểm A(1; 2) thuộc d và điểm B(-4; 0) thuộc d’ nên bị loại
Tính khoảng cách từ C tới hai đường thẳng d, d’
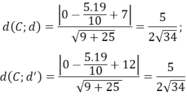
⇒ d(C;d)=d(C;d')=> C là tâm đối xứng
Nhận xét: nếu I là tâm đối xứng của hình gồm hai đường thẳng song song thì I cách đều hai đường thẳng song song đó.
Đáp án C
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng α : x + y - z - 2 = 0 và đường thẳng d : x + 1 2 = y - 1 1 = z - 2 1 Phương trình nào dưới đây là phương trình mặt phẳng chứa đường thẳng (d) và vuông góc với mặt phẳng α
A. x+y-z+2=0
B. 2x-3y-z+7=0
C. x+y+2z-4=0
D. 2x-3y-z-7=0
Đáp án B
Phương pháp giải:
Ứng dụng của tích có hướng để tìm vectơ pháp tuyến của mặt phẳng. Phương trình mặt phẳng đi qua M ( x 0 ; y 0 ; z 0 ) và có VTPT
![]()
![]()
Lời giải:
![]()
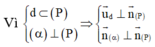
![]()
![]()
Vậy phương trình mặt phẳng (P): 2x-3y-z+7=0
Trong không gian Oxyz, cho đường thẳng d : x - 1 1 = y - 2 2 = z - 3 1 và mặt phẳng ( α ) : x + y + z - 2 = 0 Đường thẳng nằm trong mặt phẳng ( α ) , đồng thời vuông góc và cắt đườn thẳng d có phương trình là
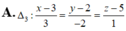
![]()
![]()
![]()