Cho tích phân  I = ∫ 0 2 f ( x ) d x = 2 . Tính tích phân  J = ∫ 0 2 3 f ( x ) - 2 d x

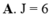
Cho hàm số f(x) thỏa mãn  ∫ 0 1 ( x + 1 ) f ' ( x ) d x = 10 và 2f(1) - f(0) = 2 .Tính tích phân  I = ∫ 0 1 f ( x ) d x .

A. I=-12.

B. I=8.

C. I=12.

D. I=-8

Cho hàm số  y = f ( x ) = x 2   k h i   0 ≤ x ≤ 1 2 - x   k h i   1 ≤ x ≤ 2

Tính tích phân I=  ∫ 0 2 f ( x ) d x

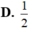
Cho hàm số y = f(x) có đạo hàm f’(x) liên tục trên đoạn [0; 1] thỏa mãn f(1) = 1 và I = ∫ 0 1 f x d x = 2 . Tính tích phân    I = ∫ 0 1 f ' x d x

A. I = -1.

B. I = 1.

C. I = 2.

D. I = -2.

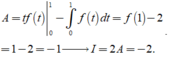
Cho hàm số y=f(x) có đạo hàm liên tục trên đoạn [ 0 ; 2 ]  và thỏa mãn  f ( 0 ) = 2 , ∫ 0 2 ( 2 x - 4 ) . f ' ( x ) d x = 4 . Tính tích phân I = ∫ 0 2 f ( x ) d x .

A.  I = 2

B.  I = - 2

C.  I = 6

D.  I = - 6

Cho tích phân I = ∫ 0 4 f ( x ) d x = 32 . Tính tích phân J = ∫ 0 2 f ( 2 x ) d x

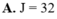
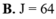
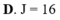
Cho hàm số f(x) liên tục trên [0;1] và f(1) – f(0) = 2. Tính tích phân  ∫ 0 1 f ' x d x .

A. I = –1

B. I = 1

C. I = 2

D. I = 0

Cho hàm số y=f(x) liên tục trên đoạn [0;π/3].Biết f’(x).cosx+f(x).sinx=1, x ϵ [0;π/3] và f(0)=1. Tính tích phân  I = ∫ 0 π 3 f x d x

A.  1/2 + π/3

B.   3 + 1 2

C.   3 - 1 2

D.  1/2

Cho hàm số y=f(x) xác định và liên tục trên  0 ; + ∞  sao cho x²+ x.f(e^x) + f(e^x)=1 với mọi x ∈ 0 ; + ∞ . Tính tích phân  I = ∫ e e ln x .   f ( x ) x d x

A. -1/8 

B. -2/3

C. 1/12 

D. 3/8