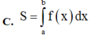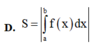Hàm số y = f(x) được cho bởi công thức y = -1,5x. Vẽ đồ thị của hàm số trên

Những câu hỏi liên quan
hàm số y = f(x) được cho bởi công thức y = -1,5x
a) Vẽ đồ thị hàm số trên
b) Bằng đồ thị hãy tìm các giá trị f(-2) , f(1) , f(2)
Hàm số y = f(x) được cho bởi công thức y = -1,5x. Bằng đồ thị hãy tìm các giá trị f(-2), f(1), f(2) (và kiểm tra lại bằng cách tính).
+) Dựa vào đồ thị ta có:
f(-2) = 3; f(1) = -1,5 và f(2)= -3
+) Kiểm tra lại bằng phép tính:
f(-2) = - 1,5. (-2)= 3.
f(1) = -1,5.1 = -1,5
f(2) = -1,5. 2 = - 3.
Đúng 0
Bình luận (0)
2. cho hàm số y=f(x) = (1/3-a)*x
a) sác định hằng số a nếu đồ thị hàm số đi qua điểm A(1;3) . viết công thức của hàm số
b) vẽ đồ thị hàm số cho bởi công thức trên
c)tính f(2004) và tính x biết f(x)=2004
MONG RẰNG NÓ SẼ GIÚP ÍCH CHO BẠN
a) Vì A(1; 3) ∈ đồ thị hàm số y = f(x) = (1313 - a)x
⇒ 3 = (1313 - a) . 1
⇒ 1313 - a = 3 : 1 = 3
⇒ a = 1313 - 3
⇒ a = 1313 - 9393 = −83−83
⇒ Ta có công thức của hàm số:
y = f(x) = (1313 - −83−83)x = 3x
b) Cho x = -1
⇒ y = 3 . (-1) = -3
⇒ B(-1; -3) ∈ đồ thị hàm số y = 3x
Bn tự vẽ nha
c) f(2004) = 3 . 2004 = 6012
f(x) = 2004 ⇒ 3x = 2004
⇒ x = 2004 : 3 = 668
a) Vì A(1; 3) ∈ đồ thị hàm số y = f(x) = (1313 - a)x
⇒ 3 = (1313 - a) . 1
⇒ 1313 - a = 3 : 1 = 3
⇒ a = 1313 - 3
⇒ a = 1313 - 9393 = −83−83
⇒ Ta có công thức của hàm số:
y = f(x) = (1/3-(-8/3))x = 3x
b) Cho x = -1
⇒ y = 3 . (-1) = -3
⇒ B(-1; -3) ∈ đồ thị hàm số y = 3x
Bn tự vẽ nha
c) f(2004) = 3 . 2004 = 6012
f(x) = 2004 ⇒ 3x = 2004
⇒ x = 2004 : 3 = 668
Cho hàm số y f(x) và hàm số bậc ba y g(x) có đồ thị như hình vẽ bên. Diện tích phần gạch chéo được tính bởi công thức nào sau đây?
A
.
S
∫
-
3
-
1
[
f
(
x
)
-
g
(
x
)
]
dx
+
∫
-
1...
Đọc tiếp
Cho hàm số y = f(x) và hàm số bậc ba y = g(x) có đồ thị như hình vẽ bên. Diện tích phần gạch chéo được tính bởi công thức nào sau đây?
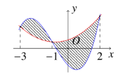
A . S = ∫ - 3 - 1 [ f ( x ) - g ( x ) ] dx + ∫ - 1 2 [ g ( x ) - f ( x ) ] dx
B . S = | ∫ - 3 2 [ f ( x ) - g ( x ) ] dx |
C. S = ∫ - 3 - 1 [ g ( x ) - f ( x ) ] dx + ∫ - 1 2 [ f ( x ) - g ( x ) ] dx
D. S = ∫ - 3 - 1 [ g ( x ) - f ( x ) ] dx + ∫ - 1 2 [ g ( x ) - f ( x ) ] dx
Đồ thị của hàm số y = f(x) là đường thẳng OA (hình dưới). Hàm số đó được cho bởi công thức nào?
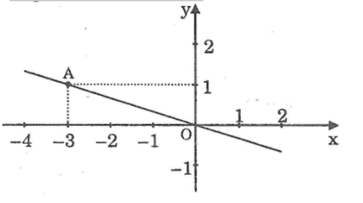
Đồ thị hàm số y = f(x) là đường thẳng OA đi qua gốc toạ độ có dạng y = ax (a≠0)
Điểm A(-3;1) thuộc đồ thị hàm số nên khi x = -3 thì y =1. Ta có: 1 = a.(-3) suy ra a =-1/3
Vậy hàm số đã cho là 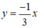
Đúng 0
Bình luận (0)
Cho hàm số y f(x) liên tục trên [a, b]. Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y f(x), trục hoành và hai đường thẳng x a; x b được tính theo công thức
Đọc tiếp
Cho hàm số y = f(x) liên tục trên [a, b]. Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a; x = b được tính theo công thức
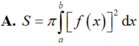
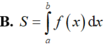
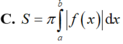

Chọn D
Hàm số y = f(x) liên tục trên [a; b]. Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a; x = b được tính theo công thức S = ∫ a b f x d x .
Đúng 0
Bình luận (0)
Cho hàm số y f(x) liên tục trên [a;b] Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số yf(x) trục hoành và hai đường thẳng xa; xb được tình theo công thức.
Đọc tiếp
Cho hàm số y = f(x) liên tục trên [a;b] Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y=f(x) trục hoành và hai đường thẳng x=a; x=b được tình theo công thức.
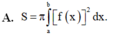
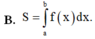
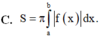
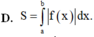
Cho hàm số y f(x) liên tục trên [a;b]. Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y f(x), trục hoành và hai đường thẳng xa, xb được tình theo công thức. A.
S
π
∫
a
b
f
x
2
d
x
.
B.
S
∫...
Đọc tiếp
Cho hàm số y = f(x) liên tục trên [a;b]. Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x=a, x=b được tình theo công thức.
A. S = π ∫ a b f x 2 d x .
B. S = ∫ a b f x d x .
C. S = π ∫ a b f x d x .
D. S = ∫ a b f x d x .
Cho hàm số y f(x) liên tục trên đoạn [a;b]. Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y f(x) trục hoành và hai đường thẳng xa; xb (ab) được tính theo công thức:
Đọc tiếp
Cho hàm số y = f(x) liên tục trên đoạn [a;b]. Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y = f(x) trục hoành và hai đường thẳng x=a; x=b (a<b) được tính theo công thức:
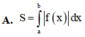
![]()