Cho hàm số y = a x 4 + b x 2 + c có đồ thị như hình vẽ bên. Tìm kết luận đúng.
A. a + b > 0
B. bc > 0
C. ab > 0
D. ac > 0
Những câu hỏi liên quan
Cho hàm số yf(x) liên tục trên K có đạo hàm f(x) Đồ thị của hàm số f(x) như hình vẽ bên. Tìm số điểm cực trị của đồ thị hàm số f(x)? A. 3 B. 1 C. 0 D. 2
Đọc tiếp
Cho hàm số y=f(x) liên tục trên K có đạo hàm f'(x) Đồ thị của hàm số f'(x) như hình vẽ bên.
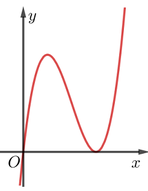
Tìm số điểm cực trị của đồ thị hàm số f(x)?
A. 3
B. 1
C. 0
D. 2
Đáp án B
f'(x) đổi dấu 1 lần, suy ra đồ thị hàm số f(x) có 1 điểm cực trị.
Đúng 0
Bình luận (0)
Cho hàm số
y
(
x
-
1
)
(
x
2
-
4
)
có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số
y
x
-
1
(
x
2
-
4
)
là hình nào dưới đây? A. Hình 1 B. Hình 2 C. Hình 3 D. Hình 4
Đọc tiếp
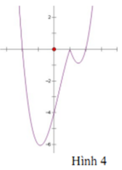
Cho hàm số y = ( x - 1 ) ( x 2 - 4 ) có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số y = x - 1 ( x 2 - 4 ) là hình nào dưới đây?
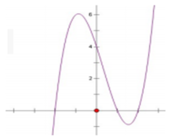
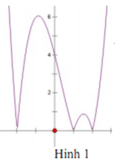
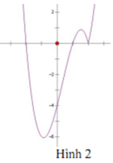
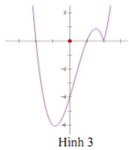
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Cho đồ thị hàm số y f(x) có đồ thị như hình vẽ bênTìm số nghiệm của phương trình f(x) x A. 0 B. 1 C. 2 D. 3
Đọc tiếp
Cho đồ thị hàm số y = f(x) có đồ thị như hình vẽ bên
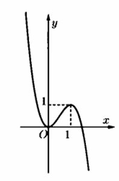
Tìm số nghiệm của phương trình f(x) = x
A. 0
B. 1
C. 2
D. 3
Cho hàm số yf(x) có đồ thị là (C), hàm số yf(x) có đồ thị như hình vẽ bên. Tiếp tuyến với (C) tại điểm có hoành độ x2 cắt (C) tại hai điểm phân biệt có hoành độ lần lượt là a,bGiá trị
(
a
-
b
)
2
thuộc khoảng nào dưới đây A.
(
0
;
9
)
B.
(
12
;
16
)
C.
(
16...
Đọc tiếp
Cho hàm số y=f(x) có đồ thị là (C), hàm số y=f'(x) có đồ thị như hình vẽ bên. Tiếp tuyến với (C) tại điểm có hoành độ x=2 cắt (C) tại hai điểm phân biệt có hoành độ lần lượt là a,b
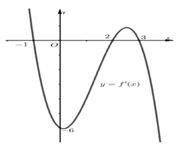
Giá trị ( a - b ) 2 thuộc khoảng nào dưới đây
A. ( 0 ; 9 )
B. ( 12 ; 16 )
C. ( 16 ; + ∞ )
D. ( 9 ; 12 )
Cho hàm số
y
f
x
ax
3
+
bx
2
+
cx
+
d
có đồ thị (C), đồ thị y f (x) như hình vẽ bên. Biết đồ thị hàm số y f(x) có điểm cực tiểu có tung độ bằng
2
3
. Tính ...
Đọc tiếp
Cho hàm số y = f x = ax 3 + bx 2 + cx + d có đồ thị (C), đồ thị y = f '(x) như hình vẽ bên. Biết đồ thị hàm số y = f(x) có điểm cực tiểu có tung độ bằng 2 3 . Tính 3 a − b + 5 c + 3 d bằng?
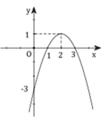
A. -16
B. -12
C. 9
D. 10
Đáp án B
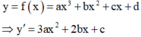
Nhìn vào đồ thị của hàm số y = f '(x) ta nhận thấy đồ thị hàm số đi qua các điểm (1;0), (3;0), (2;1) nên có hệ phương trình sau:
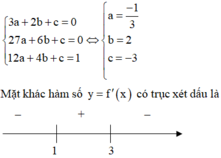
Nên đồ thị hàm số y = f(x) có điểm cực tiểu có tung độ bằng 2 3
Đúng 0
Bình luận (0)
Cho hàm số y f( x) có đồ thị như hình vẽ bên Tìm số điểm cực trị của hàm số y 2f( x) – 3f( x) A. 6 B. 5 C. 4 D. 3
Đọc tiếp
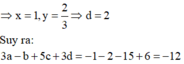
Cho hàm số y= f( x) có đồ thị như hình vẽ bên
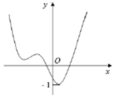
Tìm số điểm cực trị của hàm số y= 2f( x) – 3f( x)
A. 6
B. 5
C. 4
D. 3
Xét hàm số
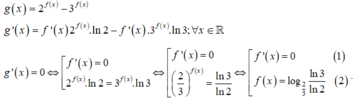
Dựa vào đồ thị hàm số y= f( x) , ta thấy:
Phương trình (1) có 3 nghiệm phân biệt (vì hàm số y= f (x) có 3 điểm cực trị).
Phương trình (2) vô nghiệm vì đường thẳng y = log 2 3 ln 3 ln 2 < - 1 không cắt ĐTHS.
Vậy phương trình g’ (x) =0 có 3 nghiệm phân biệt hay hàm số đã cho có 3 điểm cực trị.
Chọn D.
Đúng 0
Bình luận (0)
Cho hàm số yf( x) ax3+ bx2+ cx+ d có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y 4 tại điểm có hoành độ âm và đồ thị hàm số y f’(x) cho bởi hình vẽ bên. Tìm hàm số đã cho ? A. y x3-3x+2. B. yx3+3x+2. C. yx3-2x+2. D. y x3-3x-1.
Đọc tiếp
Cho hàm số y=f( x) = ax3+ bx2+ cx+ d có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y= 4 tại điểm có hoành độ âm và đồ thị hàm số y= f’(x) cho bởi hình vẽ bên. Tìm hàm số đã cho ?
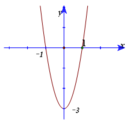
A. y =x3-3x+2.
B. y=x3+3x+2.
C. y=x3-2x+2.
D. y =x3-3x-1.
+ Ta có đạo hàm : f’ (x) = 3ax2+ 2bx+ c.
Dựa vào đồ thị hàm số y= f’( x), ta thấy đồ thị hàm số y= f’ (x) là parabol có trục đối xứng là trục tung nên b=0
Đồ thị hàm số y= f’( x) đi qua 2 điểm (1;0) và (0; -3) thay vào f’(x) ; ta tìm được: a=1 và c= -3.
Suy ra: f’(x) = 3x2-3b và f(x) = x3-3x+d.
+ Do (C) tiếp xúc với đường thẳng y= 4 tại điểm có hoành độ âm nên ta có:
f’(x) =0 khi và chỉ khi x= -1;x= 1( loại)
Như vậy (C) đi qua điểm (-1; 4) ta tìm được d= 2
Khi đó; f( x) =x3-3x+2.
chọn A.
Đúng 0
Bình luận (0)
Cho hàm số y=f(x) liên tục trên R và có đồ thị là đường cong như hình vẽ bên. Tìm điểm cực tiểu của đồ thị hàm số y=f(x).
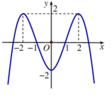
A. y=-2
B. x=0
C. M(0;-2)
D. N(2;2)
Đáp án C
Nhìn vào đồ thị thì điểm cực tiểu là điểm M(0;-2)
Đúng 0
Bình luận (0)
Cho hàm số yf(x) có đồ thị như hình vẽ bên. Biết rằng f(x) là một trong bốn phương án A, B, C, D đưa ra dưới đây. Tìm f(x). A. f(x)
x
4
-
2
x
2
B. f(x)
x
4
+
2
x
2
C. f(x)
-
x
4
+
2
x
2
-
1...
Đọc tiếp
Cho hàm số y=f(x) có đồ thị như hình vẽ bên. Biết rằng f(x) là một trong bốn phương án A, B, C, D đưa ra dưới đây. Tìm f(x).
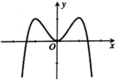
A. f(x) = x 4 - 2 x 2
B. f(x) = x 4 + 2 x 2
C. f(x) = - x 4 + 2 x 2 - 1
D. f(x) = - x 4 + 2 x 2
Cho hàm số
y
x
-
a
b
x
+
c
có đồ thị như hình vẽ bên. Tính giá trị của biểu thức A a+ b+ c A. - 2 B. -3 C. - 4 D. -5
Đọc tiếp
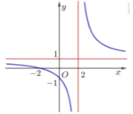
Cho hàm số y = x - a b x + c có đồ thị như hình vẽ bên. Tính giá trị của biểu thức A= a+ b+ c
A. - 2
B. -3
C. - 4
D. -5
Dựa vào đồ thị hàm số ta thấy:
Đồ thị hàm số có TCĐ và TCN là
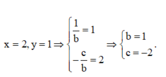
Đồ thị hàm số đi qua điểm có tọa độ ( -2; 0) nên a= -2
Suy ra A= a+ b+ c= -2+ 1+ ( -2) = -3
Chọn B.
Đúng 0
Bình luận (0)