Có tất cả bao nhiêu số nguyên m để đồ thị hàm số y = x + m x 2 + x + 1 có đường tiệm cận ngang?
A. 1.
B. 2.
C. 0.
D. vô số.
Cho hàm số y = x mũ 4 trừ 2 m bình x bình + 1 Hỏi có tất cả bao nhiêu số nguyên m để đồ thị hàm số có 2 điểm cực tiểu đều thuộc trục hoành. Giúp minh với
Trong tất cả các giá trị của m để đồ thị hàm số y = x − 4 m x 2 + m 2 − 17 có bốn đường tiệm cận, có bao nhiêu giá trị m nguyên
A. 1.
B. 2.
C. 3.
D. 4.
Trong tất cả các giá trị của m để đồ thị hàm số y = x − 4 m x 2 + m 2 − 17 có bốn đường tiệm cận, có bao nhiêu giá trị m nguyên?
A. 1
B. 2
C. 3
D. 4
Cho hàm số y=f(x) liên tục trên R có đồ thị như hình vẽ bên. Có bao nhiêu số nguyên m để phương trình f(f(x)-m)=0 có tất cả 9 nghiệm thực phân biệt.
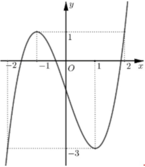
A. 1.
B. 0.
C. 3.
D. 2.
Cho hàm số y=f(x) liên tục trên ℝ có đồ thị như hình vẽ bên dưới.
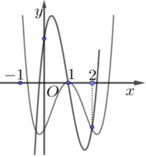
Có bao nhiêu số nguyên m để phương trình
f(f(x) - m) = 0 có tất cả 9 nghiệm thực phân biệt?
A. 1
B. 0
C. 3
D. 2
Cho hàm số y = x - 1 m x 2 - 2 x + 3 . Có tất cả bao nhiêu giá trị m để đồ thị hàm số có đúng hai đường tiệm cận?
A.0
B.1
C.2
D.3
Cho hàm số y = x - 1 m x 2 - 2 x + 3 . Có tất cả bao nhiêu giá trị m để đồ thị hàm số có đúng hai đường tiệm cận?
A. 0.
B. 1.
C. 2.
D. 3.
Chọn D.
![]() nên đồ thị hàm số luôn có 1 tiệm cận ngang.
nên đồ thị hàm số luôn có 1 tiệm cận ngang.
Do đó đồ thị hàm số cần có đúng 1 tiệm cận đứng.
+ m = 0, đồ thị hàm số có 1 tiệm cận đứng là đường thẳng x = 3 2 => m = 0 thỏa mãn bài toán.
+ m
≠
0 , đồ thị hàm số có đúng 1 tiệm cận đứng khi và chỉ khi phương trình ![]() có nghiệm kép hoặc có hai nghiệm phân biệt trong đó có nghiệm x = 1.
có nghiệm kép hoặc có hai nghiệm phân biệt trong đó có nghiệm x = 1.
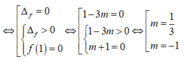
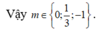
Cho hàm số y = x - 1 m x 2 - 2 x + 3 . Có tất cả bao nhiêu giá trị m để đồ thị hàm số có đúng hai đường tiệm cận
A. 2
B. 3
C. 0
D. 1
Có tất cả bao nhiêu giá trị nguyên của m ≥ - 10 sao cho đồ thị hàm số y = x 2 + x - 1 x 2 + ( m - 1 ) x + 1 có đúng một tiệm cận đứng?
A. 11.
B. 10.
C. 12.
D. 9.
Điều kiện: 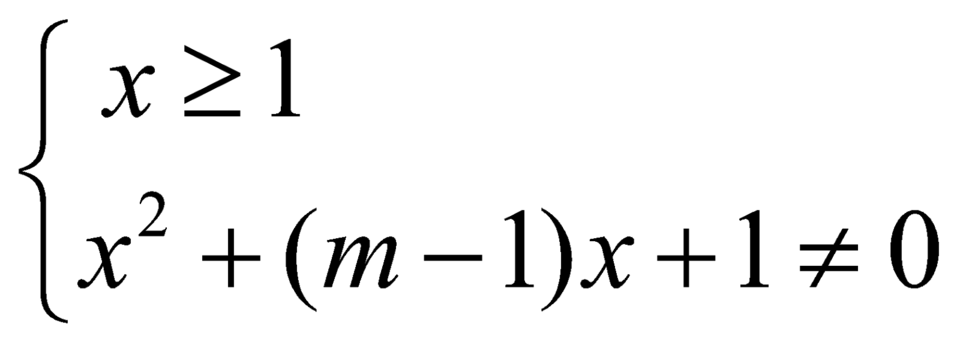
Ta thấy ![]()
⇒ đồ thị hàm số có đúng một TCĐ![]() có đúng một nghiệm
có đúng một nghiệm ![]()
TH1: Phương trình (*) có nghiệm kép

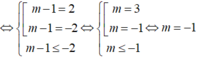
TH2: Phương trình (*) có 2 nghiệm phân biệt ![]()
![]()
Kết hợp các TH và điều kiện bài cho trước ![]() ta có:
ta có: ![]() thỏa mãn điều kiện bài toán
thỏa mãn điều kiện bài toán
Chọn D
Chú ý khi giải: Chú ý điều kiện ![]()