Đối với hàm số y = ln 1 x + 1 , khẳng định nào sau đây là khẳng định đúng?
A. x y ' − 1 = − e y
B. x y ' + 1 = − e y
C. x y ' − 1 = e y
D. x y ' + 1 = e y
Đối với hàm số y = ln ( 1 x + 1 ) , khẳng định nào sau đây là khẳng định đúng?
A. x y ' + 1 = - e y
B. x y ' + 1 = e y
C. x y ' - 1 = e y
D. x y ' - 1 = - e y
Cho hàm số y = x – ln(1 + ex). Khẳng định nào sau đây là đúng?
A. Hàm số đạt cực đại tại x = 0
B. Tập xác định của hàm số là D = (0; +∞)
C. Hàm số đồng biến trên R
D. Hàm số đạt cực tiểu tại x = 1
Chọn C.
y' = 1 – 1/e > 0 suy ra hàm đồng biến trên R
Đối với hàm số y = ln 1 x + 1 , khẳng định nào sau đây là khẳng định đúng?
A . x y ' + 1 = - e y
B . x y ' + 1 = e y
C . x y ' - 1 = e y
D . x y ' - 1 = - e y
Chọn B
Hàm số
y
=
ln
1
x
+
1
có tập xác định ![]()
Khi đó
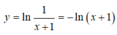
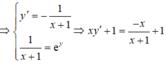
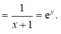
Cho hàm số y = ln x. Khẳng định nào sau đây là khẳng định sai?
A. Hàm số đồng biến trên khoảng 0 ; + ∞
B. Hàm số có tập giá trị là - ∞ ; + ∞
C. Đồ thị hàm số nhận trục Oy làm tiệm cận đứng
D. Hàm số có tập giá trị là 0 ; + ∞
Đáp án D
Hàm số y = ln x có tập giá trị là ℝ .
Cho hàm số y = ln x. Khẳng định nào sau đây là khẳng định sai?
A. Hàm số đồng biến trên khoảng 0 ; + ∞
B. Hàm số có tập giá trị là - ∞ ; + ∞
C. Đồ thị hàm số nhận trục Oy làm tiệm cận đứng
D. Hàm số có tập giá trị là 0 ; + ∞
Đáp án D
Hàm số y = ln x có tập giá trị là R
Với hàm số y = ln 1 x + 1 , khẳng định nào sau đây là khẳng định đúng?
![]()
![]()
![]()
![]()
Cho hàm số y = x + 1 x - 1 ( 1 )
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số (1) nghịch biến trên R\{1}
B. Hàm số (1) nghịch biến trên (-∞; 1) và (1; +∞)
C. Hàm số (1) nghịch biến trên (-∞; 1) ∪ (1; +∞)
D. Hàm số (1) đồng biến trên (-∞; 1) và (1; +∞)
Chọn B
Hàm số
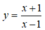
xác định ∀x ≠ 1
Ta có:
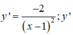
xác định ∀x ≠ 1
Bảng xét dấu đạo hàm
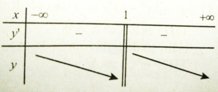
Hàm số nghịch biến trên các khoảng (-∞; 1) và (1; +∞)
Cho hàm số y = x + 1 x − 1 . Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số đồng biến trên khoảng − ∞ ; 1 và nghịch biến trên khoảng 1 ; + ∞
B. Hàm số nghịch biến trên R \ 1
C. Hàm số nghịch biến trên các khoảng − ∞ ; 1 và 1 ; + ∞
D. Hàm số nghịch biến trên R
Đáp án C
Ta có y ' = − 2 x − 1 2 < 0 ∀ ≠ 1 ⇒ hàm số nghịch biến trên các khoảng − ∞ ; 1 và 1 ; + ∞
Cho hàm số y = x − 2 x − 1 . Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số nghịch biến trên ℝ \ 1 .
B. Hàm số đồng biến trên ℝ \ 1 .
C. Hàm số đơn điệu trên ℝ
D. Hàm số đồng biến trên các khoảng − ∞ ; 1 và 1 ; + ∞
Đáp án D
Phương pháp:
Hàm số dạng y = a x + b c x + d luôn đồng biến hoặc nghịch biến trên từng khoảng xác định của nó.
Cách giải: Tập xác định D = ℝ \ 1
Ta có: y ' = − 1 + 2 x − 1 2 = 1 x − 1 2 > 0 ∀ x ∈ ℝ
Vậy hàm số đồng biến trên các khoảng − ∞ ; 1 và 1 ; + ∞