Các câu hỏi tương tự
Cho hàm số f(x)
a
x
4
+
b
x
3
+
c
x
2
+
d
x
+
e
, với a,b,c,d,e
∈
ℝ
. Hàm số y f(x) có đồ thị như hình vẽ. Trong các khẳng định sau, khẳng định nào đúng? A. a + b + c + d 0. B. a + c b + d C. a + c 0 D. d + b - c 0
Đọc tiếp
Cho hàm số f(x) = a x 4 + b x 3 + c x 2 + d x + e , với a,b,c,d,e ∈ ℝ . Hàm số y = f'(x) có đồ thị như hình vẽ. Trong các khẳng định sau, khẳng định nào đúng?
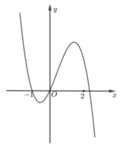
A. a + b + c + d < 0.
B. a + c < b + d
C. a + c > 0
D. d + b - c > 0
Cho hàm số
y
e
.
x
-
e
-
x
, khẳng định nào sau đây đúng? A. Hàm số nghịch biến trên R B. Hàm số đạt cực tiểu tại
x
-
1
C. Hàm số đạt cực đại tại
x
-...
Đọc tiếp
Cho hàm số y = e . x - e - x , khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên R
B. Hàm số đạt cực tiểu tại x = - 1
C. Hàm số đạt cực đại tại x = - 1
D. Hàm số đồng biến trên R
Cho hàm số
y
x
+
1
x
-
1
(
1
)
Khẳng định nào sau đây là khẳng định đúng? A. Hàm số (1) nghịch biến trên R{1} B. Hàm số (1) nghịch biến trên (-∞; 1) và (1; +∞) C. Hàm số (1) nghịch biến trên (-∞; 1) ∪ (1; +∞) D. Hàm số (1) đồng biến trên (-∞; 1) và (1; +∞)
Đọc tiếp
Cho hàm số y = x + 1 x - 1 ( 1 )
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số (1) nghịch biến trên R\{1}
B. Hàm số (1) nghịch biến trên (-∞; 1) và (1; +∞)
C. Hàm số (1) nghịch biến trên (-∞; 1) ∪ (1; +∞)
D. Hàm số (1) đồng biến trên (-∞; 1) và (1; +∞)
Cho hàm số y f( x) ax4+ bx3+ cx2+ dx+ e với a≠0. Đồ thị hàm số y f’(x) như hình bên. Khẳng định nào sau đây sai? A. Hàm số y f(x) đồng biến trên ( -2; 1) B. Hàm số y f( x) đồng biến trên (1; + ∞) C. Hàm số y f(x) nghịch biến trên đoạn có độ dài nhỏ hơn 1000. D. Hàm số y f( x) nghịch biến trên (- ∞; -2)
Đọc tiếp
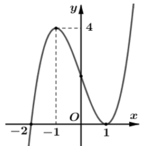
Cho hàm số y= f( x) = ax4+ bx3+ cx2+ dx+ e với a≠0. Đồ thị hàm số y= f’(x) như hình bên. Khẳng định nào sau đây sai?
A. Hàm số y= f(x) đồng biến trên ( -2; 1)
B. Hàm số y= f( x) đồng biến trên (1; + ∞)
C. Hàm số y= f(x) nghịch biến trên đoạn có độ dài nhỏ hơn 1000.
D. Hàm số y= f( x) nghịch biến trên (- ∞; -2)
Cho hàm số yf(x) liên tục trên R thỏa mãn
∫
f
(
x
)
d
x
e
-
2018
x
+
C
. Khẳng định nào sau đây là đúng?
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R thỏa mãn ∫ f ( x ) d x = e - 2018 x + C . Khẳng định nào sau đây là đúng?
![]()
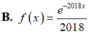
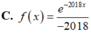
![]()
Cho hàm số y(x+1)/(x-2).Khẳng định nào sau đây là đúng? A. Hàm số đồng biến trên khoảng B. Hàm số nghịch biến trên R. C. Hàm số đồng biến trên D. Hàm số nghịch biến trên khoảng
Đọc tiếp
Cho hàm số y=(x+1)/(x-2).Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng ![]()
B. Hàm số nghịch biến trên R.
C. Hàm số đồng biến trên ![]()
D. Hàm số nghịch biến trên khoảng ![]()
Cho hàm số yf(x), yg(x),
y
f
x
+
3
g
x
+
1
. Hệ số góc của các tiếp tuyến của các đồ thị hàm số đã cho tại điểm có hoành độ x1 bằng nhau và khác 0. Khẳng định nào dưới đây là khẳng định đúng A.
f
1
≤
−
11...
Đọc tiếp
Cho hàm số y=f(x), y=g(x), y = f x + 3 g x + 1 . Hệ số góc của các tiếp tuyến của các đồ thị hàm số đã cho tại điểm có hoành độ x=1 bằng nhau và khác 0. Khẳng định nào dưới đây là khẳng định đúng
A. f 1 ≤ − 11 4
B. f 1 < − 11 4
C. f 1 > − 11 4
D. f 1 ≥ − 11 4
Cho hàm số y f(x) có
1
≤
f
(
x
)
≤
4
với mọi
x
∈
2
;
5
. Hỏi khẳng định nào dưới đây là khẳng định đúng? A.
3
≤
f
(
5
)
-
f
(
2
)
≤
12
B.
-
12
≤...
Đọc tiếp
Cho hàm số y = f(x) có 1 ≤ f ' ( x ) ≤ 4 với mọi x ∈ 2 ; 5 . Hỏi khẳng định nào dưới đây là khẳng định đúng?
A. 3 ≤ f ( 5 ) - f ( 2 ) ≤ 12
B. - 12 ≤ f ( 5 ) - f ( 2 ) ≤ 3
C. 1 ≤ f ( 5 ) - f ( 2 ) ≤ 4
D. - 4 ≤ f ( 5 ) - f ( 2 ) ≤ - 1
Cho hàm số
y
x
+
1
(
x
-
2
)
. Khẳng định nào sau đây là khẳng định sai? A. Hàm số nghịch biến trên khoảng
(
-
1
;
1
2
)
. B. Hàm số nghịch biến trên khoảng
(
-
∞
;
-
1...
Đọc tiếp
Cho hàm số y = x + 1 ( x - 2 ) . Khẳng định nào sau đây là khẳng định sai?
A. Hàm số nghịch biến trên khoảng ( - 1 ; 1 2 ) .
B. Hàm số nghịch biến trên khoảng ( - ∞ ; - 1 ) .
C. Hàm số đồng biến trên các khoảng ( - ∞ ; - 1 ) v à ( 1 2 ; + ∞ ) .
D. Hàm số nghịch biến trên khoảng ( - 1 ; 1 2 ) và đồng biến trên khoảng ( 1 2 ; + ∞ ) .