Phương trình cos2x+4 sinx+5=0 có bao nhiêu nghiệm trên khoảng ( 0 ; 10 π )
A. 5
B. 4
C. 2
D. 3
Những câu hỏi liên quan
Phương trình cos2x+4sinx+50 có bao nhiêu nghiệm trên khoảng
(
0
;
10
π
)
A. 5 B. 4 C. 2 D. 3
Đọc tiếp
Phương trình cos2x+4sinx+5=0 có bao nhiêu nghiệm trên khoảng ( 0 ; 10 π )
A. 5
B. 4
C. 2
D. 3
Đáp án A
Dùng công thức
cos
2
x
=
1
-
2
sin
2
x
để đưa phương trình ban đầu về đa thức bậc 2 theo sin x.
Giải phương trình này tìm x và đối chiếu với yêu cầu
x
∈
0
;
10
π
để tìm được giá trị của x.
Ta có
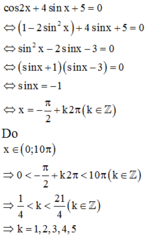
Do đó tập nghiệm của phương trình đã cho trên ( 0 ; 10 π ) là
Đúng 0
Bình luận (0)
Phương trình cos 2 x + 4 sin x + 5 = 0 có bao nhiêu nghiệm trên khoảng 0 ; 10 π
A. 5
B. 4
C. 2
D. 3
Phương trình cos2x+4sinx+50 có bao nhiêu nghiệm trên khoảng
0
;
10
π
A. 2 B. 3 C. 4 D. 5
Đọc tiếp
Phương trình cos2x+4sinx+5=0 có bao nhiêu nghiệm trên khoảng 0 ; 10 π
A. 2
B. 3
C. 4
D. 5
Phương trình
cos
2
x
+
4
sin
x
+
5
0
có bao nhiêu nghiệm trên khoảng
0
;
10
π
? A. 2 B. 3 C. 4 D. 5
Đọc tiếp
Phương trình cos 2 x + 4 sin x + 5 = 0 có bao nhiêu nghiệm trên khoảng 0 ; 10 π ?
A. 2
B. 3
C. 4
D. 5
Đáp án D
PT
⇔ 1 − 2 sin 2 x + 4 sin x + 5 = 0 ⇔ sin 2 x − 2 sin x − 3 = 0 ⇔ sin x = − 1 sin x = 3
⇒ sin x = − 1 ⇔ x = − π 2 + k 2 π k ∈ ℤ
Vì
x ∈ 0 ; 10 π ⇔ 0 < − π 2 + k 2 π < 10 π ⇔ 1 4 < k < 21 4 ⇒ k ∈ 1 ; 2 ; 3 ; 4 ; 5
Đúng 0
Bình luận (0)
Phương trình cos 2 x + 2 cos x − 3 = 0 có bao nhiêu nghiệm trong khoảng 0 ; 2019 ?
A. 1009
B. 1010
C. 320
D. 321
Phương trình cos 2 x + 2 cos x - 3 = 0 có bao nhiêu nghiệm trong khoảng (0;2019)
A. 320
B. 1009
C. 1010
D. 321
Phương trình cos2x + 2cosx - 3 = 0 có bao nhiêu nghiệm trong khoảng (0;2019) ?
A. 320
B. 1009
C. 1010
D. 321
Phương trình cos 2 x + cos x = 0 có bao nhiêu nghiệm thuộc khoảng − π ; π
A. 1
B. 4
C. 2
D. 3
Đáp án C.
Phương pháp
Sử dụng tính chất hai góc bù nhau cos x = cos π − x
Giải phương trình lượng giác cơ bản
Cách giải
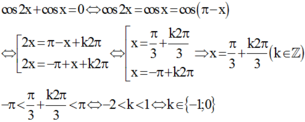
Vậy phương trình có 2 nghiệm thuộc − π ; π
Đúng 0
Bình luận (0)
Cho hàm số y = cos2x + sinx. Phương trình y’ = 0 có bao nhiêu nghiệm thuộc khoảng (0; π)
A. 1 nghiệm.
B. 2 nghiệm.
C. 3 nghiệm.
D. 4 nghiệm.
Chọn C.
y' = -2cosxsinx + cosx = cosx(1 – 2sinx)
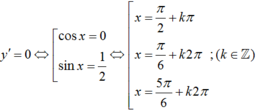
Vì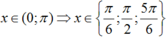 
. Vậy có 3 nghiệm thuộc khoảng (0; π).
Đúng 0
Bình luận (0)