Trong không gian Oxyz, cho hai mặt phẳng (P): 2x+y+mz-2=0 và (Q): x+ny+2z+8=0 song với nhau. Giá trị của m và n lần lượt là :
A. 4 và 1/2
A. 2 và 1/2
C. 2 và 1/4
D. 4 và 1/4
Những câu hỏi liên quan
Trong không gian Oxyz, cho hai mặt phẳng (P): 2x+y+mz-20 và (Q): x+ny+2z+80 song với nhau. Giá trị của m và n lần lượt là : A. 4 và
1
2
B. 2 và
1
2
C. 2 và
1
4
D. 4 và
1
4
Đọc tiếp
Trong không gian Oxyz, cho hai mặt phẳng (P): 2x+y+mz-2=0 và (Q): x+ny+2z+8=0 song với nhau. Giá trị của m và n lần lượt là :
A. 4 và 1 2
B. 2 và 1 2
C. 2 và 1 4
D. 4 và 1 4
Đáp án A
Phương pháp : Cho hai mặt phẳng có phương trình lần lượt là :
Khi đó (P) và (Q) song song với nhau
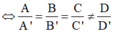
Cách giải:
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P) : 2x + 3y – mz – 2 0 và (Q) : x + y + 2z + 1 0. Tìm m để hai mặt phẳng (P) và (Q) vuông góc với nhau A.
m
5
2
B.
m
3
2
C.
m
9
2
D.
m
9
2
Đọc tiếp
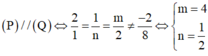
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P) : 2x + 3y – mz – 2 = 0 và (Q) : x + y + 2z + 1 = 0. Tìm m để hai mặt phẳng (P) và (Q) vuông góc với nhau
A. m = 5 2
B. m = 3 2
C. m = 9 2
D. m = 9 2
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng
(
P
)
:
2
x
+
3
y
–
m
z
–
2
0
v
à
(
Q
)
:
x
+
y
+
...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng ( P ) : 2 x + 3 y – m z – 2 = 0 v à ( Q ) : x + y + 2 z + 1 = 0 . Tìm m để hai mặt phẳng (P) và (Q) vuông góc với nhau.
A. m = 5 2
B. m = 3 2
C. m = 9 2
D. m = 7 2
Trong không gian Oxyz, cho hai mặt phẳng (P) và (Q) lần lượt có phương trình là x - y + 2z 0; 2x - 2y + (
m
2
+ 3m)z +
m
2
- m 0, trong đó m là tham số. Với những giá trị nào của m thì hai mặt phẳng (P) và (Q) song song? A. m 1 B. m -4 C. m 1 hoặc m -4 D. m 0
Đọc tiếp
Trong không gian Oxyz, cho hai mặt phẳng (P) và (Q) lần lượt có phương trình là x - y + 2z = 0; 2x - 2y + ( m 2 + 3m)z + m 2 - m = 0, trong đó m là tham số. Với những giá trị nào của m thì hai mặt phẳng (P) và (Q) song song?
A. m = 1
B. m = -4
C. m = 1 hoặc m = -4
D. m = 0
Đáp án B
Vecto pháp tuyến của hai mặt phẳng (P) và (Q) là :
n p → (1; -1; 2); n q → (2; -2; m2 + 3m)
Hai mặt phẳng (P) và (Q) song song với nhau khi và chỉ khi tồn tại một số thực k sao cho:
n p → = k. n q →
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho hai mặt phẳng (P) và (Q) lần lượt có phương trình là mx + y - 3z + 1 0; 4x - 2y + (
n
2
+ n)z - n 0, trong đó m và n là hai tham số. Với những giá trị nào của m và n thì hai mặt phẳng (P) và (Q) song song với nhau A. m-2 và n2 B. m2 và n-3 C. m-2 và n2 hoặc n-3 D. m-2 và n-3
Đọc tiếp
Trong không gian Oxyz, cho hai mặt phẳng (P) và (Q) lần lượt có phương trình là mx + y - 3z + 1 = 0; 4x - 2y + ( n 2 + n)z - n = 0, trong đó m và n là hai tham số. Với những giá trị nào của m và n thì hai mặt phẳng (P) và (Q) song song với nhau
A. m=-2 và n=2
B. m=2 và n=-3
C. m=-2 và n=2 hoặc n=-3
D. m=-2 và n=-3
Đáp án D
Hai mặt phẳng đã cho song song khi và chỉ khi tồn tại một số thực k sao cho:
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm
A
0
;
−
1
;
−
1
,
B
−
1
;
−
3
;
1
. Giả sử C,D là 2 điểm di động thuộc mặt phẳng
P...
Đọc tiếp
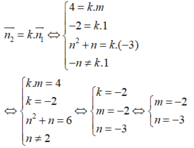
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A 0 ; − 1 ; − 1 , B − 1 ; − 3 ; 1 . Giả sử C,D là 2 điểm di động thuộc mặt phẳng P = 2 x + y − 2 z − 1 = 0 sao cho CD = 4 và A,C,D thẳng hàng. Gọi S 1 , S 2 lần lượt là diện tích lớn nhất và nhỏ nhất của tam giác BCD. Khi đó tổng S 1 + S 2 có giá trị bằng bao nhiêu?
A. 34 3
B. 17 3
C. 11 3
D. 37 3
Đáp án A
Gọi H là hình chiếu vuông góc của B lên đường thẳng CD, khi đó ta có
Do đó yêu cầu bài toán trở thành tìm H để khoảng cách BH là lớn nhất hay nhỏ nhất.
Ta thấy BH nhỏ nhất đúng bằng khoảng cách từ B đến mp (P), ta có
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho hai mặt phẳng
α
:
x
+
2
y
−
z
−
1
0
và
β
:
2
x
+
4
y
−
m
z
−
2
0.
Tìm m để hai mặt phẳng
α
v
à
β
song song với nhau. A. m...
Đọc tiếp
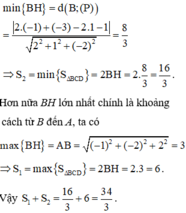
Trong không gian Oxyz, cho hai mặt phẳng α : x + 2 y − z − 1 = 0 và β : 2 x + 4 y − m z − 2 = 0. Tìm m để hai mặt phẳng α v à β song song với nhau.
A. m = 1
B. Không tồn tại m
C. m = -2
D. m = 2
Trong không gian Oxyz, cho hai đường thẳng d:
x
-
2
+
4
t
y
1
-
4
t
z...
Đọc tiếp
Trong không gian Oxyz, cho hai đường thẳng d: x = - 2 + 4 t y = 1 - 4 t z = - 2 + 3 t ; ∆ : x = - 2 + t ' y = 1 + n t ' z = - 2 + t ' và mặt phẳng (P): 2x-y+2z+1=0. Biết rằng ∆ song song với (P) và ∆ tạo với d một góc bé nhất, khi đó giá trị của biểu thức m 2 + n 2
A. 4.
B. 13.
C. 8.
D. 25.
Trong không gian
O
x
y
z
cho mặt cầu
(
s
)
:
(
x
-
1
)
2
+
(
y
-
2
)
2
+
(
z
-
1...
Đọc tiếp
Trong không gian O x y z cho mặt cầu ( s ) : ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 1 ) 2 = 6 tiếp xúc với hai mặt phẳng ( P ) : x + y + 2 z + 5 = 0 , ( Q ) : 2 x - y + z - 5 = 0 lần lượt tại A và B. Độ dài đoạn thẳng AB là
A. 2 6
B. 3
C. 3 2
D. 2 3
