Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy và S A = a 3 . Góc giữa đường thẳng SD và mặt phẳng (ABCD) bằng:
A. arcsin 3 5
B. 45 0
C. 60 0
D. 30 0
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy và SA=a 3 . Tính thể tích V của khối chóp S.ABCD
A. V= 3 a 3
B. V= 3 3 a 3
C. V= a 3
D. V=1/3 a 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, SA = a 3 . Tính thể tích hình chóp S.ABCD.
A. a 3 3
B. a 3 3 3
C. a 3 3
D. 3 a 3 3
Phương pháp:
Thể tích khối chóp có chiều cao h và diện tích đáy S là ![]()
Cách giải:
Diện tích đáy ![]()
Thể tích khối chóp là
![]()
Chọn B.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy (ABCD) và SA =a 3 . Khi đó, thể tích của khối chóp bằng:
A. a 3 3 3
B. a 3 3 4
C. a 3 3
D. a 3 3 6
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và SA vuông góc với đáy, SA=2a Tính theo a thể tích khối chóp S.ABCD
![]()
![]()
![]()

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy và SA=a. Tính theo a thể tích V của khối chóp S.ABCD.
A. V = a 3
B. V = 1 6 a 3
C. V = 1 2 a 3
D. V = 1 3 a 3
Cho hình chóp S.ABCD có đáy
ABCD là hình vuông cạnh a, SA
vuông góc với mặt đáy và SA=a.
Mặt cầu ngoại tiếp hình chóp
S.ABCD có bán kính bằng
![]()
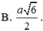
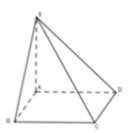
![]()
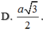
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy và SA = a 3 . Góc giữa đường thẳng SD và mặt phẳng (ABCD) bằng:
A. arcsin 3 5
B. 45 °
C. 60 °
D. 30 °
Chọn C.
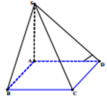
Vì SA ⊥ (ABCD) nên góc giữa đường thẳng SD và mặt phẳng (ABCD) là góc S D A ^
Tam giác SAD vuông tại A nên ![]()
Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh bằng a. Cạnh SA vuông góc với mặt phẳng đáy (ABCD), SA=a 3 . Góc tạo với mặt phẳng (SAB) và (SCD) bằng
![]()
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh bằng a. Cạnh SA vuông góc với mặt phẳng đáy (ABCD), SA=a 3 . Góc tạo với mặt phẳng (SAB) và (SCD) bằng
A. 300
B. 600
C. 900
D. 450
Đáp án A
Do AB // CD => giao tuyến của mặt phẳng (SAB) và (SCD) là đường thẳng qua S và song song với AB.
Dễ thấy Sx ⊥ (DSA) => Góc tạo bởi mặt phẳng (SAB) và (SCD) bằng góc D S A ^ = a r c tan 1 3 = 30 0
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy (ABCD) và S C = a 5 . Tính thể tích khối chóp S.ABCD
A. V = a 3 3 3 .
B. V = a 3 3 6 .
C. V = a 3 3 .
D. V = a 3 15 3 .