Tìm tất cả các giá trị thực của tham số m để phương trình sau có nghiệm x ∈ [ 1 ; 2 ] .
x 4 + 16 x 4 + 4 ( x 2 + 4 x 2 ) - 12 ( x - 2 x ) = m
A. - 13 ≤ m ≤ 11
B. - 15 ≤ m ≤ 9
C. - 15 < m < 9
D. - 16 ≤ m ≤ 9
Tìm tất cả các giá trị thực của tham số m để phương trình sau có nghiệm: 2 x 2 + x + m 2 − 2 m = 0 .
A. m = 1 2 .
B. m = 3
C. m = 1
D. m = 3 4 .
Đáp án C
Đặt t = x ≥ 0 , khi đó PT đã cho trở thành 2 t 2 + t + m 2 − 2 m = 0 ⇔ 2 t 2 + t = − m 2 + 2 m
Hàm số y = 2 t 2 + t đồng biến trên 0 ; + ∞ .
Để PT đã cho có nghiệm thì − m 2 + 2 m ≥ y 0 ⇔ − m 2 + 2 m ≥ 1 ⇔ m − 1 2 ≤ 0 ⇔ m = 1
Cho bất phương trình 3 + x + 1 - x ≤ m + 1 - x 2 - 2 x . Tìm tất cả các giá trị thực của tham số m để bất phương trình có nghiệm thực.
A. m ≥ 25 4
B. m ≥ 4
C. m ≥ 6
D. m ≥ 7
Cho phương trình log 2 x = m với x > 0. Tìm tất cả các giá trị thực của tham số m để phương trình có nghiệm thực.
A. m ≥ 0
B. m ∈ ℝ
C. m > 0
D. m ∈ ℤ
Đáp án là B
Tập giá trị của hàm số log a x = R
Cho phương trình log 2 m = m với x > 0. Tìm tất cả các giá trị thực của tham số m để phương trình có nghiệm thực
A. m ≥ 0
B. m ∈ R
C. m > 0
D. < 0
Tìm tất cả các giá trị thực của tham số m để bất phương trình log 1 2 x - 1 > log 1 2 x 3 + x - m có nghiệm
A. mÎR
B. m < 2
C. m ≤ 2
D. Không tồn tại m
Tìm tất cả các giá trị thực của tham số m để phương trình sau có nghiệm 2 m cos x + sin x = 2 m 2 + cos x − sin x + 3 2
A. − 1 2 < m < 1 2
B. m = ± 1 2
C. − 1 4 < m < 1 4
D. m = ± 1 4
Tìm tất cả các giá trị thực của tham số m để phương trình log 2 5 x - 1 . log 4 2 . 5 x - 2 = m có nghiệm x ≥ 1
A. m ∈ (-∞;2)
B. m ∈ (2;+∞)
C. m ∈ (3;+∞)
D. m ∈ (-∞;3)
Đáp án C
Phương pháp:

![]() phương trình trở thành
phương trình trở thành
![]()
![]()
![]()
=> Hàm số đồng biến trên khoảng [2;+∞)
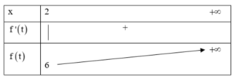
Để phương trình (*) có nghiệm thì 2m ≥ 6 ⇔ m ≥ 3
Tìm tất cả các giá trị thực của tham số m để phương trình log 2 5 x - 1 . log 4 2 . 5 x - 2 = m có nghiệm x ≥1?
A. m ϵ [2;+∞).
B. m ϵ [3;+∞).
C. m ϵ (-∞;2].
D. m ϵ (-∞;3].
Tìm tất cả các giá trị thực của tham số m để phương trình x . log 2 x − 1 + m = m . log 2 x − 1 + x có hai nghiệm thực phân biệt.
A. m > 1 v à m ≠ 2
B. m ≠ 3
C. m > 1 v à m ≠ 3
D. m > 1
Đáp án C
Ta có: x . log 2 x − 1 + m = m . log 2 x − 1 + x
⇔ x − m . log 2 x − 1 = x − m .
⇔ x − m log 2 x − 1 − 1 ⇔ x − m = 0 log 2 x − 1 = 1 ⇔ x = m x − 1 = 2 ⇔ x = m x = 3 *
Để phương trình đã cho có 2 nghiệm phân biệt ⇔ * có nghiệm duy nhất x > 1 ; x ≠ 3. Vậy m > 1 v à m ≠ 3 là giá trị cần tìm.
Cho hàm số y = f(x) có bảng biến thiên như sau:
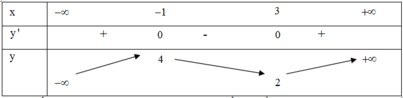
Tìm tất cả các giá trị thực của tham số m để phương trình f(x) = m + 1 có 3 nghiệm thực phân biệt?
A. –3 ≤ m ≤ 3
B. –2 ≤ m ≤ 4
C. –2 < m < 4
D. –3 < m < 3
Đáp án D
Phương pháp:
Đánh giá số nghiệm của phương trình f(x) = m + 1 bằng số giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = m + 1
Cách giải:
Số nghiệm của phương trình f(x) = m + 1 bằng số giao điểm của đồ thị hàm số y = f(x)
và đường thẳng y = m + 1
Để f(x) = m + 1 có 3 nghiệm thực phân biệt thì –2 < m+1 < 4 ó –3 < m < 3