Cho khối S.ABC có góc A S B ^ = B S C ^ = C S A ^ = 60 ° và S A = 2 , S B = 3 , S C = 4. Tính thể tích khối S.ABC.
A. 2 2
B. 2 3
C. 4 3
D. 3 2
Cho hình chóp S.ABC có đáy là tam giác vuông cận tại B , AB = a . Cạnh bên SA vuông góc với mặt phẳng (ABC) và SC hợp với đáy một góc bằng 60 0 . Gọi (S) là mặt cầu ngoại tiếp khối chóp S.ABC. Tính thể tích khối cầu (S).
A. 8 2 πa 3 3
B. 4 2 πa 3 3
C. 2 2 πa 3 3
D. 2 πa 3 3
Đáp án A
Gọi M là trung điểm của AC. Tam giác ABC vuông tại B, do đó M là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi O là trung điểm của AC, suy ra OM // SA. Mà

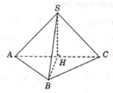
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, đỉnh S cách đều các điểm A,B,C. Biết AC = 2a,BC = a; góc giữa đường thẳng SB và mặt đáy (ABC) bằng 60 o . Tính theo a thể tích V của khối chóp S.ABC?
A. V = a 6 3 4 .
B. V = a 6 3 6 .
C. V = a 3 2 .
D. V = a 6 3 12 .
Đáp án C.
Hướng dẫn giải: Gọi H là trung điểm AC.
Do tam giác ABC vuông tại B nên H là tâm đường tròn ngoại tiếp tam giác ABC.
Đỉnh S cách đều các điểm A, B,C nên hình chiếu của S trên mặt đáy (ABC) trùng với tâm đường tròn ngoại tiếp tam giác ABC
suy ra S H ⊥ ( A B C )
![]()
Tam giác vuông SBH, có
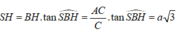
Tam giác vuông ABC ,
có A B = A C 2 - B C 2 = a 3
Diện tích tam giác vuông
S ∆ A B C = 1 2 B A . B C = a 3 2 2
Vậy V S . A B C = 1 3 S ∆ A B C . S H = a 3 2
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, AB=d. Cạnh bên SA vuông góc với mặt phẳng (ABC) và SC hợp với đáy một góc bằng 60°. Gọi (S) là mặt cầu ngoại tiếp khối chóp S.ABC. Tính thể tích khối cầu (S).
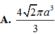
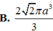
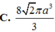
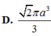
Trong không gian với hệ tọa độ Oxyz, cho S(1;2;3) và các điểm A , B , C thuộc các trục Ox ,Oy , Oz sao cho hình chóp S.ABC có các cạnh SA, SB, SC đôi một vuông góc với nhau. Thể tích khối chóp S.ABC là?
☺☻♥♦♣♠•◘○◙♂♀♪♫☼►◄↕‼¶§▬↨↑↓→←2◘↔▲▼ !"#◘%&'Ü)*+,-./0123;
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AB = a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết góc giữa SB và mặt phẳng (ABC) bằng 450.
A. a 3 3 4
B. a 3 3 12
C. a 3 2 12
D. a 3 2 4
Đáp án C
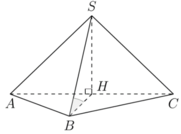
Gọi H là trung điểm AC. Ta có tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với (ABC)
suy ra S H ⊥ A B C
Ta có
S B , A B C = S B H ^ = 45 o ⇒ S H = B H = 1 2 A C = a 2 2 V S . A B C = 1 3 . a 2 2 . 1 2 a 2 = a 3 2 12
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AB = a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết góc giữa SB và mặt phẳng (ABC) bằng 450
A. a 3 3 4
B. a 3 3 12
C. a 3 2 12
D. a 3 2 4
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 1, góc giữa cạnh bên và mặt đáy bằng 60 ∘ Gọi A ' , B ' , C ' lần lượt là các điểm đối xứng của A,B,C qua S. Thể tích của khối đa diện A B C A ' B ' C ' bằng
A. V = 2 3 3
B. V = 2 3
C. V = 4 3 3
D. V = 3 2
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 1, góc giữa cạnh bên và mặt đáy bằng 60 o C . Gọi A',B',C' lần lượt là các điểm đối xứng của A,B,C qua S. Thể tích của khối đa diện ABCA'B'C' bằng
A. V = 2 3 3
B. V = 2 3
C. V = 4 3 3
D. V = 3 2
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 1, góc giữa cạnh bên và mặt đáy bằng 60 0 . Gọi A',B',C' lần lượt là các điểm đối xứng của A,B,C qua S. Thể tích của khối đa diện ABCA'B'C' bằng
A. V = 2 3 3
B. V = 2 3
C. V = 4 3 3
D. V = 3 3
Cho hình chóp S.ABC có tam giác ABC vuông tại A, BC = 2a, góc ACB = 60 ° . Mặt phẳng (SAB) vuông góc với mặt phẳng (ABC), tam giác SAB cân tại S, tam giác SBC vuông tại S. Thể tích khối chóp S.ABC là:
A. a 3 2
B. a 3 4
C. a 3 8
D. a 3 16