Cho hình lập phương A B C D . A ' B ' C ' D ' cạnh bằng 2 a . Gọi K là trung điểm của DD'. Tính khoảng cách giữa hai đường thẳng CK và A'D'.
A. a 3
B. 2 a 5 5
C. 2 a 3 3
D. 4 a 3 3
Những câu hỏi liên quan
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Khoảng cách giữa hai đường thẳng AB,C′D′ bằng
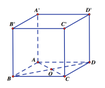
A. 2 a
B. a
C. 3 a
D. 3 2 a
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Khoảng cách giữa hai đường thẳng AB,C′D′ bằng A.
a
2
B. a. C.
a
3
D.
a
3
2
Đọc tiếp
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Khoảng cách giữa hai đường thẳng AB,C′D′ bằng
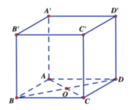
A. a 2
B. a.
C. a 3
D. a 3 2
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Khoảng cách giữa hai đường thẳng AB,C′D′ bằng A.
2
a
B.
a
C.
3
a
D.
a
3
2
Đọc tiếp
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Khoảng cách giữa hai đường thẳng AB,C′D′ bằng
A. 2 a
B. a
C. 3 a
D. a 3 2
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Khi đó thể tích hình chóp A.A'BCD' bằng:
A. a 3 /2 B. a 3 /3
C. a 3 /4 D. a 3 /6
Chọn B.
Hình nón A.A'BCD' với đáy là hình chữ nhật A'BCD' có diện tích S = A'B.BC = a 2 √2 và chiều cao h = (a 2 )/2 nên có thể tích V = a 3 /3
Đúng 0
Bình luận (0)
a. Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa 2 đường thẳng AC và AH
b. Cho hình lập phương ABCD.A'B'C'D'. Số do góc giữa 2 đường thẳng A'B và B'C là?
c. Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Gọi I vàJ lần lượt là trung điểm của SC và BC. Số đo góc (IJ,CD) là?
d. Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa 2 vecto AF và EG?
a. Gọi cạnh lập phương là a
Ta có: \(AC=\sqrt{AB^2+AD^2}=a\sqrt{2}\)
\(AH=\sqrt{AD^2+DH^2}=a\sqrt{2}\)
\(CH=\sqrt{CD^2+DH^2}=a\sqrt{2}\)
\(\Rightarrow\Delta ACH\) đều \(\Rightarrow\widehat{CAH}=60^0\)
b.
Do \(B'C||A'D\Rightarrow\) góc giữa A'B và B'C bằng góc giữa A'B và A'D
Tương tự câu a, ta có tam giác A'BD đều \(\Rightarrow\widehat{BA'D}=60^0\)
c.
Do IJ song song SB (đường trung bình), CD song song AB \(\Rightarrow\) góc giữa IJ và CD bằng góc giữa SB và AB
Tam giác SAB đều (các cạnh bằng a) \(\Rightarrow\widehat{SBA}=60^0\)
d.
\(\overrightarrow{EG}=\overrightarrow{AC}\Rightarrow\widehat{\left(\overrightarrow{AF};\overrightarrow{EG}\right)=\widehat{\left(\overrightarrow{AF};\overrightarrow{AC}\right)}=\widehat{FAC}=60^0}\) do tam giác FAC đều
Đúng 1
Bình luận (1)
Cho hình lập phương ABCD.A′B′C′D′ cạnh a. Khoảng cách từ điểm A đến mặt phẳng (A′B′CD) bằng A.
a
2
B.
3
a
C.
3
3
a
D.
2
2
a
Đọc tiếp
Cho hình lập phương ABCD.A′B′C′D′ cạnh a. Khoảng cách từ điểm A đến mặt phẳng (A′B′CD) bằng
A. a 2
B. 3 a
C. 3 3 a
D. 2 2 a
Gọi O là tâm của hình vuông
A D D ' A ' ⇒ A O ⊥ A ' B ' C D ⇒ d A , A ' B ' C D = A O = 2 a 2
Chọn đáp án D.
Đúng 0
Bình luận (0)
Cho hình lập phương ABCD.A′B′C′D′ cạnh a. Khoảng cách giữa hai đường thẳng BD và A′C′ bằng A.
2
a. B. a. C.
3
a. D.
2
a
2
Đọc tiếp
Cho hình lập phương ABCD.A′B′C′D′ cạnh a. Khoảng cách giữa hai đường thẳng BD và A′C′ bằng
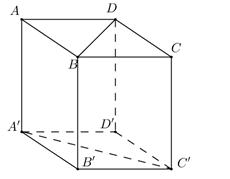
A. 2 a.
B. a.
C. 3 a.
D. 2 a 2
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Tính diện tích xung quanh của hình trụ có hai đường tròn đáy ngoại tiếp hai hình vuông ABCD và A′B′C′D′. A.
S
πa
2
2
2
B.
S
2
πa
2
C.
S
π
2...
Đọc tiếp
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Tính diện tích xung quanh của hình trụ có hai đường tròn đáy ngoại tiếp hai hình vuông ABCD và A′B′C′D′.
A. S = πa 2 2 2
B. S = 2 πa 2
C. S = π 2 a 2
D. S = πa 2
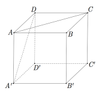
hình lập phương ABCD.A′B′C′D′ cạnh a. Khoảng cách giữa hai đường thẳng AC và A′D bằng A.
2
2
a B.
3
3
a C.
3
6
a D.
2
3
a
Đọc tiếp
hình lập phương ABCD.A′B′C′D′ cạnh a. Khoảng cách giữa hai đường thẳng AC và A′D bằng
A. 2 2 a
B. 3 3 a
C. 3 6 a
D. 2 3 a
Cho hình lập phương ABCD.A′B′C′D′ cạnh bằng a. Khoảng cách giữa hai đường thẳng BD và CC′ bằng A. a/2. B.
a
2
4
C.
a
2
2
D. a/4.
Đọc tiếp
Cho hình lập phương ABCD.A′B′C′D′ cạnh bằng a. Khoảng cách giữa hai đường thẳng BD và CC′ bằng
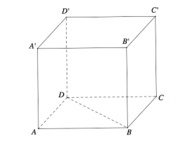
A. a/2.
B. a 2 4
C. a 2 2
D. a/4.
