Cho tứ diện đều S.ABC là trung điểm của canh BC Khi đó cos( AB,DM) bằng:
A. 3 6
B. 2 2
C. 3 2
D. 1 2
Cho tứ diện đều ABCD, M là trung điểm của cạnh BC. Khi đó cos(AB, DM) bằng
A. 3 6
B. 2 2
C. 3 2
D. 1 2
Cho tứ diện đều ABCD, M là trung điểm của cạnh BC. Khi đó cos(AB, DM) bằng:
A . 3 6
B . 2 2
C . 3 2
D . 1 2
Cho tứ diện đều ABCD, M là trung điểm của cạnh BC. Khi đó cos (AB, DM) bằng
A. 3 6
B. 2 2
C. 3 2
D. 1 2
Cho tứ diện đều ABCD, M là trung điểm của cạnh BC. Khi đó cos (AB, DM) bằng:
A. 3 6
B. 2 2
C. 3 2
D. 1 2
Cho tứ diện đều ABCD có cạnh bằng a, M là trung điểm của cạnh BC. Gọi α là góc giữa hai đường thẳng AB và DM, khi đó c o s α cbằng
A . 3 6
B . 2 2
C . 3 2
D . 1 2
Cho tứ diện đều ABCD, M là trung điểm của cạnh BC. Khi đó c o s A B , D M bằng
A. 3 6
B. 2 2
C. 3 2
D. 1/2
Đáp án A
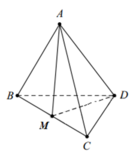
Xét tứ diện đều ABCD canh a ⇒ D M = a 3 2 ; A M = a 3 2
Ta có c os A B ¯ ; D M ¯ = A B ¯ . D M ¯ A B ¯ . D M ¯ = A B ¯ . D M ¯ a . a 3 2 = 2 3 . A B ¯ . D M ¯ a 2
Mà A B ¯ . D M ¯ = A B ¯ A M ¯ − A D ¯ = A B ¯ . A M ¯ − A B ¯ . A D ¯
= A B . A M . c os A B ¯ ; A M ¯ − A B . A D . c os A B ¯ ; A D ¯ = a . a 3 2 . 3 2 − a 2 2 = a 2 4
Vậy c os A B ¯ . D M ¯ = 3 6 > 0 ⇒ c os A B ; D M = 3 6 .
Cho tứ diện đều ABCD Cạnh a M là trung điểm của BC tính cos(AB,DM)
(hình bạn tự vẽ lấy nha)
\(\widehat{\left(AB,DM\right)}\) = \(\widehat{\left(AB,\left(BCD\right)\right)}\) = \(\widehat{\left(AO,BO\right)}\)
( với O là chân đường cao hạ thừ đỉnh S xuống trọng tâm đáy)
=> cos (AB,DM) = cos (AO,BO) =\(cos\widehat{\left(ABO\right)}\) = \(\dfrac{BO}{AB}\)(*)
vì BO = \(\dfrac{2}{3}\) đg cao tam giác đáy => BO= \(a\dfrac{\sqrt{3}}{3}\)
thay vào (*) ta đk cos = \(\dfrac{\sqrt{3}}{3}\)
Cho tứ diện đều S.ABC. Gọi I là trung điểm của AB, M là một điểm lưu động trên đoạn AI. Qua M vẽ mặt phẳng (∝) //(SIC). Khi đó thiết diện của mặt phẳng (∝) và tứ diện S.ABC là:
A. tam giác cân tại M
B. tam giác đều
C. hình bình hành
D. hình thoi
Đáp án A
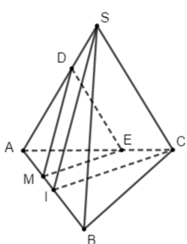
Qua M kẻ đường thẳng song song với IC cắt AC tại E và kẻ đường thẳng song song với SI cắt SA tại D.
Khi đó thiết diện của mặt phẳng với tứ diện là tam giác MED
Lại có: MD // SI ⇒ A M A I = M D S I
ME // IC ⇒ A M A I = M E I C
Do đó M D S I = M E I C
Vì S.ABC là tứ diện đều nên SI = CI (hai đường trung tuyến trong hai tam giác đều có chung cạnh)
Suy ra MD = ME
Vậy tam giác MED cân tại M.
Đáp án B
Cho tứ diện ABCD có ABC và DBC là hai tam giác đều cạnh chung BC = 2. Gọi I là trung điểm của BC, A I D ^ = 2 α mà cos 2 α = - 1 3 . Hãy xác định tâm O của mặt cầu ngoại tiếp tứ diện đó.
A. O là trung điểm của AD.
B. O là trung điểm của BD.
C. O thuộc mặt phẳng (ADB).
D. O là trung điểm của AB.
Chọn A.
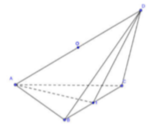
![]() và
và ![]() nên
nên ![]()
Pitago đảo dễ dàng suy ra tam giác ACD và tam giác ABD vuông có chung cạnh huyền AD.
Vậy tâm cầu ngoại tiếp tứ diện là trung điểm O của AD.