Xét các số phức w,z thỏa mãn | w + i | = 3 5 5 và 5 w = ( 2 + i ) ( z - 4 ) . Tìm giá trị lớn nhất của biểu thức P = | z - 2 i | + | z - 6 - 2 i |
A. 7.
B . 2 53 .
C . 2 58 .
D . 4 13 .
Xét các số phức z thỏa mãn |z+1+i| = 3.Đặt w = z + 2i -3. Tìm Max |w|
A. Max = 9
B.Max = 8
C. Max = 6
D. Max =5
Xét các số phức z thỏa mãn |z+1+i| = 3.Đặt w = z + 2i -3. Tìm Max |w|
A. Max = 9
B.Max = 8
C. Max = 6
D. Max =5
Xét các số phức z thỏa mãn điều kiện z - 3 + 2 i = 5 Trong mặt phẳng tọa độ Oxr, tập hợp các điểm biểu diễn các số phức w = z + 1 -i là
A. Đường tròn tâm I(4;-3), bán kính R = 5.
B. Đường tròn tâm I(-4;3), bán kính R = 5.
C. Đường tròn tâm I(-2;1), bán kính R = 5.
D. Đường tròn tâm I(3;-2), bán kính R = 5.
Số phức z thỏa mãn z = 5 và số phức w = ( 1 + i ) z ¯ Tìm w
A. 10
B. 2 + 5
C. 5
D. 2 5
Đáp án A
Phương pháp: Cho
z
1
,
z
2
là hai số phức bất kì, khi đó ![]()
Cách giải: Ta có:
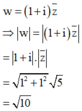
Cho số phức z thỏa mãn |z| = 5 và số phức w = ( 1 + i ) z Tìm |w|
A. 10
B. 2 + 5
C. 5
D. 2 5
Đáp án A
Phương pháp: Cho z1, z2 là hai số phức bất kì, khi đó | z1.z2 | = |z1|.|z2|
Cách giải: Ta có:
![]()
![]()
xét các số phức z, w thỏa mãn \(\left|z\right|=1\) và \(\left|w\right|=2\). khi \(\left|z+i\overline{w}-6+8i\right|\) đạt GTNN, \(\left|z-w\right|\) = ?
Xét các số phức z, w thỏa mãn z + 2 − 2 i = z − 4 i và w = i z + 1 . Giá trị nhỏ nhất của w bằng?
A. 2
B. 2 2
C. 3 2 2
D. 2 2
Các số phức z, w thay đổi nhưng thỏa mãn |z + i – 2i| = 1 và |w - 3 + i| = 3. Tìm |z - w|max
A. |z - w|max = 2.
B. |z - w|max = 4.
C. |z - w|max = 9.
D. |z - w|max = 10.
số phức z thỏa mãn z = 5 và số phức w = 1 + i z Tìm w
![]()
![]()
C. 5
![]()