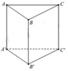
Cho lăng trụ đều A B C . A ' B ' C ' có tất cả các cạnh bằng a (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng AC và BB’ bằng
A. 5 a 3
B. 2 a 5
C. a 5
D. 3 a 2
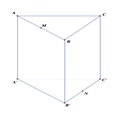
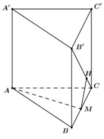
Cho hình lăng trụ tam giác đều ABC.A′B′C′ có tất cả các cạnh bằng a. Gọi M,N lần lượt là trung điểm các cạnh AB,B′C′ (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng MN và AC bằng
A. 1 3
B. 5 3
C. 2 3
D. 5 5
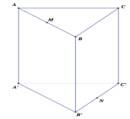
Cho hình lăng trụ tam giác đều ABC.A′B′C′ có tất cả các cạnh bằng a. Gọi M,N lần lượt là trung điểm các cạnh AB,B′C′ (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng MN và AC bằng
A. 1 3 .
B. 5 3 .
C. 2 3 .
D. 5 5 .
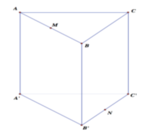
Cho hình lăng trụ tam giác đều ABC.A′B′C′ có tất cả các cạnh bằng a. Gọi M,N lần lượt là trung điểm các cạnh AB,B′C′ (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng MN và AC bằng
A. 1 3
B. 5 3
C. 2 3
D. 5 5
Đáp án D
Gọi P là trung điểm cạnh BC
![]()
Tam giác MPN vuông tại P có
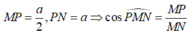
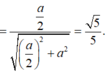
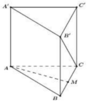
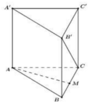
Cho hình lăng trụ đều ABC.A'B'C' có tất cả các cạnh bằng a (tham khảo hình vẽ bên). Gọi M là trung điểm của cạnh BC. Khoảng cách giữa hai đường thẳng AM và B’C là:
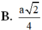
![]()
![]()
Cho hình lăng trụ đều ABC.A’B’C’ có tất cả các cạnh bằng a (tham khảo hình vẽ bên). Gọi M là trung điểm của cạnh BC. Khoảng cách giữa hai đường thẳng AM và B’C là:
A. a 2 2
B. a 2 4
C. a
D. a 2
Đáp án B
Phương pháp : Dụng đường vuông góc chung.
Cách giải :
Ta có: 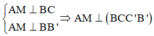
Trong (BCC’B’) kẻ ![]()
![]()
=>MH là đoạn vuông góc chung giữa AM và B’C ![]()
Dễ thấy 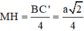
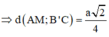
Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng 2. Gọi M,N,P lần lượt là trung điểm các cạnh AB,BB′ và A’C’ (tham khảo hình vẽ bên). Thể tích của khối tứ diện CMNP bằng
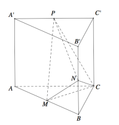
A. 5 3 12
B. 2 3 3
C. 5 3 4
D. 5 3 8
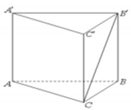
Cho lăng trụ tam giác đều ABC.A'B'C' có tất các cạnh bằng a (tham khảo hình vẽ). Tính theo a khoảng cách giữa hai đường thẳng AA' và B'C.
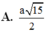
![]()
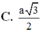
![]()
Cho lăng trụ tam giác đều A B C . A ' B ' C ' có tất các cạnh bằng a (tham khảo hình vẽ). Tính theo a khoảng cách giữa hai đường thẳng AA' và B'C
A. a 15 2
B. a 2
C. a 3 2
D. a
Đáp án C
d A A ' , C B ' = d A A ' , C B B ' C ' = d A , C B B ' C ' = a 3 2
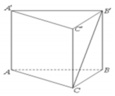
Cho lăng trụ đứng ABC. A’B’C’ có tất cả các cạnh bằng a và có G, G' lần lượt là trọng tâm của hai tam giác ABC và A’B’C’ (tham khảo hình vẽ).
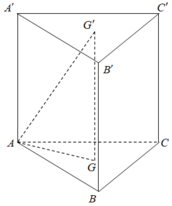
Thiết diện tạo bởi mặt phẳng (AGG') với hình lăng trụ đã cho là
A. Tam giác vuông
B. Tam giác cân
C. Hình vuông
D. Hình chữ nhật
Chọn D
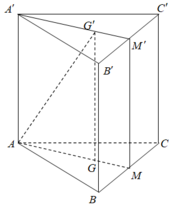
Gọi M, M' lần lượt là trung điểm của BC và B’C’. Khi đó thiết diện của lăng trụ tạo bởi mặt phẳng (AGG') là hình chữ nhật AMM'A’.
Mà A M ’ = a . s i n 60 0 = a 3 2 ≠ A A ’
Nên AMM’A’ không thể là hình vuông.