Cho hàm số y=xsinx số nghiệm thuộc - π 2 ; 2 π của phương trình y"+y=1 là
A.2
B.0
C.1
D.3
Những câu hỏi liên quan
Cho hàm số y = cos2x + sinx. Phương trình y’ = 0 có bao nhiêu nghiệm thuộc khoảng (0; π)
A. 1 nghiệm.
B. 2 nghiệm.
C. 3 nghiệm.
D. 4 nghiệm.
Chọn C.
y' = -2cosxsinx + cosx = cosx(1 – 2sinx)
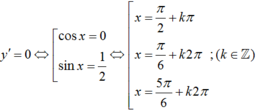
Vì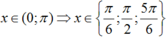 
. Vậy có 3 nghiệm thuộc khoảng (0; π).
Đúng 0
Bình luận (0)
Cho hàm số y = cos2x + sinx. Phương trình y’ = 0 có bao nhiêu nghiệm thuộc khoảng (0; π)
A. 1 nghiệm.
B. 2 nghiệm.
C. 3 nghiệm.
D. 4 nghiệm.
Cho hàm số yf(x) liên tục trên
ℝ
và có đồ thị như hình bên. Phương trình f( 2 sin x) m có đúng ba nghiệm phân biệt thuộc đoạn
-
π
;
π
khi và chỉ khi A.
m
∈
-
3
;
1
B.
m
∈
-...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình bên. Phương trình f( 2 sin x) = m có đúng ba nghiệm phân biệt thuộc đoạn - π ; π khi và chỉ khi
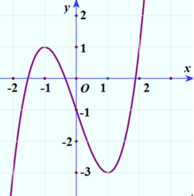
A. m ∈ - 3 ; 1
B. m ∈ - 3 ; 1
C. m ∈ [ - 3 ; 1 )
D. m ∈ ( - 3 ; 1 ]
cho hàm số y=(x-1)/(x+1) (C)
1,Khảo sát sự biến thiên và vẽ đồ thị hàm số
2,Tìm m để phương trình có nghiệm thuộc (0;π) : ((sinx-1)/(sinx+1))=m
Cho hàm số yf(x) liên tục trên R và có đồ thị như hình bên. Phương trình f(2sinx)m có đúng ba nghiệm phân biệt thuộc đoạn [-π;π] khi và chỉ khi A.
m
∈
{
-
3
;
1
}
. B.
m
∈
(
-
3
;
1
)
C.
m
∈
[
-
3
;
1
)
D.
m...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình bên. Phương trình f(2sinx)=m có đúng ba nghiệm phân biệt thuộc đoạn [-π;π] khi và chỉ khi
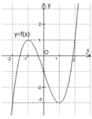
A. m ∈ { - 3 ; 1 } .
B. m ∈ ( - 3 ; 1 )
C. m ∈ [ - 3 ; 1 )
D. m ∈ ( - 3 ; 1 ]
Chọn đáp án A
Phương pháp
+) Đặt t=2sinx, xác định điều kiện của t.
+) Khi đó phương trình trở thành f(t)=m. Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y=f(t) và đường thẳng y=m song song với trục hoành.
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y=f(t) và đường thẳng y=m song song với trục hoành.
⇒ Phương trình f(t)=m có 1 nghiệm t=2 và một nghiệm t ∈ - 2 ; 2 hoặc phương trình f(t)=m có 1 nghiệm t=-2 và một nghiệm t ∈ - 2 ; 2 .
Đúng 0
Bình luận (0)
Cho hàm số yf(x) liên tục trên
ℝ
và có đồ thị như hình bên. Phương trình f(2sin x) m có đúng ba nghiệm phân biệt thuộc đoạn
-
π
;
π
khi và chỉ khi A.
m
∈
-
3
;
1
B.
m
∈
-...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình bên. Phương trình f(2sin x) = m có đúng ba nghiệm phân biệt thuộc đoạn - π ; π khi và chỉ khi
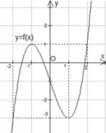
A. m ∈ - 3 ; 1
B. m ∈ - 3 ; 1
C. m ∈ [ - 3 ; 1 )
D. m ∈ ( - 3 ; 1 ]
Đạo hàm của hàm số
y
x
sin
x
bằng A.
y
sin
x
−
x
cos
x
B.
y
sin
x
+
x
cos
x
C.
y
x
cos
x
D.
y
−
x
cos
x
Đọc tiếp
Đạo hàm của hàm số y = x sin x bằng
A. y ' = sin x − x cos x
B. y ' = sin x + x cos x
C. y ' = x cos x
D. y ' = − x cos x
Đáp án B
Ta có:
y ' = sin x + x sin x ' = sin x + x cos x
Đúng 0
Bình luận (0)
Đạo hàm của hàm số y = xsinx bằng
A. y' = sinx-xcosx
B. y' = sinx + xcosx
C. y' = xcosx
D. y' = -xcosx
Đạo hàm của hàm số y xsinx bằng: A.
y
sin
x
-
x
cos
x
B.
y
sin
x
+
x
cos
x
C.
y
-
x
cos
x
D.
y
x
cos
x
Đọc tiếp
Đạo hàm của hàm số y = xsinx bằng:
A. y ' = sin x - x cos x
B. y ' = sin x + x cos x
C. y ' = - x cos x
D. y ' = x cos x
