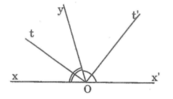
Số đo góc tạo bởi hai tia phân giác của hai góc kề bù bằng

Những câu hỏi liên quan
Với hai góc kề bù ta có định lý sau: Hai tia phân giác của hai góc kề bù tạo thành một góc vuông
Hãy vẽ hai góc xOy và yOx’ kề bù, tia phân giác Ot của góc xOy, tia phân giác Ot’ của góc yOx’ và gọi số đo của góc xOy là mº.
góc tạo bởi 2 tia phân giác của hai góc kề bù,bằng bao nhiêu ?
góc tạo bởi hai tia phân giác của hai góc kề bù là?
Góc tạo bởi hai tia phân giác của hai góc kề bù bằng bao nhiêu ?vì sao?
Nay ban, to viet dau (gach cheo''/'') la phan nhe!
Goc tao boi hai tia phan giac cua goc ke bu bang 900
Vi Goc ke bu co tong so do bang 1800
Muon tinh goc tao boi hai tia phan giac cua hai goc ke bu ta chi viec lay:
1800x1/2=900
Đúng 0
Bình luận (0)
góc tạo bởi 2 tia phân giác của hai góc kề bù, bằng bao nhiêu? Vì sao?
Hai góc kề bù có tổng số đo là 1800
=> Góc tạo bởi 2 tia p/giác của hai góc kề bù bằng nửa tổng số đo của chúng:
= 1/2 . 1800 = 900 (tạo thành góc vuông).
Đúng 0
Bình luận (0)
góc tạo bởi 2 tia phân giác của hai góc kề bù bằng bao nhiêu? vì sao
=90 độ
vì 90độ là góc vuông (cũng chả biết giải thích làm sao nữa, nhưng hầu như bài toán nào cũng thế)
Đúng 0
Bình luận (0)
90 độ
vì góc kề bù có số đo là 180 độ mà tạo bởi hai tia phân giác thi mỗi góc đương nhiên = 90 độ
Đúng 0
Bình luận (0)
Chứng tỏ rằng góc tạo bởi hai tia phân giác của hai góc kề bù bằng\(90^0\)
Gọi \(\widehat{xOz}\), \(\widehat{zOy}\) là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của \(\widehat{xOz}\) , \(\widehat{zOy}\)
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy, nên:
\(\hept{\begin{cases}\widehat{uOz}=\widehat{xOu}=\frac{\widehat{xOz}}{2}\\\widehat{zOv}=\widehat{yOv}=\frac{\widehat{zOy}}{2}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}2\widehat{uOz}=\widehat{xOz}\\2\widehat{zOv}=\widehat{zOy}\end{cases}}\)
Ta lại có:
\(\widehat{xOz}+\widehat{zOy}=180^0\) ( kề bù )
\(\Rightarrow2\widehat{uOz}+2\widehat{zOv}=180^0\)
\(\Rightarrow2\left(\widehat{uOz}+\widehat{zOv}\right)=180^0\)
\(\Rightarrow\left(\widehat{uOz}+\widehat{zOv}\right)=180^0\div2\)
\(\Rightarrow\left(\widehat{uOz}+\widehat{zOv}\right)=90^0\)
\(\Rightarrow\widehat{uOv}=90^0\) (vì 2 góc uOz, góc zOv kề nhau)
\(\Rightarrow\) Tia Ou vuông góc tia Ov
Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.
Đúng 0
Bình luận (0)
ta có góc AOE+EOC=180
MÀ BOC=AOB, OED=DOC
vậy BOC+DOE=\(\frac{AOE+EOC}{2}=\frac{180}{2}=90\)
Đúng 0
Bình luận (0)
À mk quên kí hiệu 2 góc phân giác bằng nhau
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chứng minh rằng góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông.
Xem thêm câu trả lời
chứng minh định lí:
góc tạo bởi 2 tia phân giác của hai góc kề bù bằng 90 độ
Ta có: \(\widehat{xOm}=\widehat{mOz}=\frac{\widehat{xOz}}{2}\) (vì Om là tia phân giác của xOz)
\(\widehat{zOn}=\widehat{nOy}=\frac{\widehat{yOz}}{2}\) (vì On là tia phân giác của yOz)
Có: \(\widehat{mOn}=\widehat{mOz}+\widehat{zOn}=\frac{\widehat{xOz}}{2}+\frac{\widehat{yOz}}{2}=\frac{\widehat{xOz}+\widehat{yOz}}{2}=\frac{180^o}{2}=90^o\)
=> Om _|_ On (đpcm)
Đúng 0
Bình luận (0)
mOz=12ˆxOzˆmOz=12^xOz^ (1)(1) ( vì Om là hai tia phân giác của xOzˆxOz^ )
zOnˆ=12zOyˆzOn^=12zOy^ (2)(2) ( vì On là hai tia phân giác của zOyˆzOy^ )
Từ (1)(1) và (2)(2) , ta có :
mOzˆ+zOnˆ=12.(xOzˆ+zOyˆ)mOz^+zOn^=12.(xOz^+zOy^) (3)(3)
Vì tia OzOz nằm giữa hai tia Om,OnOm,On và vì xOzˆxOz^ và zOyˆzOy^ kề bù (gt)(gt)
Nên từ (3)(3) ⇒mOnˆ=12.1800⇒mOn^=12.1800
Hay mOnˆ=900