Cho hình lăng trụ tam giác đều A B C . A ' B ' C ' có góc giữa hai mặt phẳng A ' B C và A B C bằng 60 ° , cạnh A B = a . Tính thể tích V của khối lăng trụ A B C . A ' B ' C ' ?
A. V = a 3 3 4 .
B. V = 3 a 3 4 .
C. V = 3 a 3 3 8 .
D. V = a 3 3 .
Cho hình lăng trụ tam giác đều ABC.A′B′C′ có góc giữa hai mặt phẳng (A′BC) và (ABC) bằng 60 0 , cạnh AB = 2. Thể tích V của khối lăng trụ ABC.A′B′C′ là
A. 3 3 4
B. 3
C. 3
D. 3 3
Cho hình lăng trụ tam giác đều ABC.A′B′C′ có tất cả các cạnh bằng a. Tang của góc giữa đường thẳng AB′ và mặt phẳng (ACC′A′) bằng
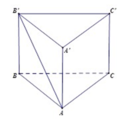
A. 1.
B. 15 5
C. 15 3
D. 6 2
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có AB = a, góc giữa hai mặt phẳng (A’BC) và (ABC) bằng 60 độ. Tính thể tích khối lăng trụ đã cho.
A. 3 3 4 a 3
B. 3 4 a 3
C. 3 3 8 a 3
D. 3 8 a 3
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có \(AB = a\), góc giữa hai mặt phẳng \(\left( {A'BC} \right)\) và \(\left( {ABC} \right)\) bằng \({60^ \circ }\).
a) Tính khoảng cách giữa hai đáy của hình lăng trụ.
b) Tinh thể tích của khối lăng trụ.

a) Gọi \(I\) là trung điểm của \(BC\).
Tam giác \(ABC\) đều \( \Rightarrow AI \bot BC\)
Tam giác \(A'BC\) cân tại \(A' \Rightarrow A'I \bot BC\)
\( \Rightarrow \left( {\left( {A'BC} \right),\left( {ABC} \right)} \right) = \left( {A'I,AI} \right) = \widehat {AI{\rm{A}}'} = {60^ \circ }\)
Tam giác \(ABC\) đều \( \Rightarrow AI = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\)
\( \Rightarrow AA' = AI.\tan \widehat {AI{\rm{A}}'} = \frac{{3a}}{2}\)
b) \({S_{\Delta ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4}\)
\({V_{ABC.A'B'C'}} = {S_{\Delta ABC}}.AA' = \frac{{3{a^3}\sqrt 3 }}{8}\)
Cho hình lăng trụ tam giác đều ABC.A'B'C' có góc giữa hai mặt phẳng (A'BC) và (ABC) bằng 60 0 , cạnh AB = a. Thể tích V của khối lăng trụ đó là:
A . 3 3 8 a 3
B . 3 a 3
C . 3 4 a 3
D . 3 4 a 3
Đáp án A
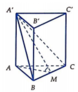
Gọi M là trung điểm BC. Ta có A ' M A ^ = 60 0
AM là trung tuyến trong tam giác đều cạnh a nên AM = a 3 2
![]()
![]()
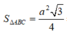
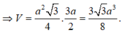
Cho hình lăng trụ tam giác ABC.A'B'C'có tất cả các cạnh bên và cạnh đáy đều bằng a. Các cạnh bên của lăng trụ tạo với mặt phẳng đáy góc 60 ο và hình chiếu vuông góc của đỉnh A lên mặt phẳng (A'B'C') trùng với trung điểm của cạnh B'C'.
a) Tính khoảng cách giữa hai mặt phẳng đáy của lăng trụ.
b) Chứng minh rằng mặt bên BCC'B' là một hình vuông.
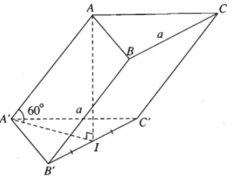
a) Gọi I là trung điểm của cạnh B'C'. Theo giả thiết ta có AI ⊥ (A'B'C') và ∠ A A ′ I = 60 ο . Ta biết rằng hai mặt phẳng (ABC) và (A'B'C') song song với nhau nên khoảng cách giữa hai mặt phẳng chính là khoảng cách AI.
Do đó
b) 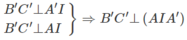
⇒ B′C′ ⊥ AA′
Mà AA′ // BB′ // CC′ nên B’C’ ⊥ BB’
Vậy mặt bên BCC’B’ là một hình vuông vì nó là hình thoi có một góc vuông.
Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh a.hình chiếu vuông góc của A' trên mặt phẳng (ABC) là trung điểm của cạnh AB, góc giữa A'C và mặt phẳng đáy là 60°.tính theo a thể tính hình lăng trụ và khoảng từ B đến mặt phẳng (ACA'C')
Cho hình lăng trụ tam giác đều ABC. A'B'C' có góc giữa hai mặt phẳng (A'BC) và (ABC) bằng 600, cạnh AB=a. Tính thể tích V của khối lăng trụ ABC. A'B'C'.
A. V = 3 4 a 3
B. V = 3 4 a 3
C. V = 3 3 a 3 8
D. V = 3 a 3
Chọn C
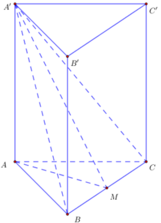
Gọi M là trung điểm của BC
=> AM ⊥ BC (1)
Ta có B C ⊥ A M B C ⊥ A A ' ⇒ B C ⊥ A ' M ( 2 )
Mặt khác A B C ∩ A ' B C = B C ( 3 )
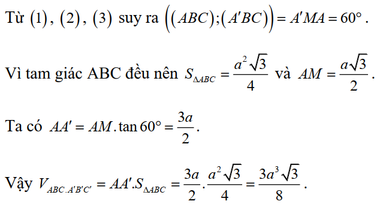
Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh a,cạnh bên bằng ![]() thì góc giữa hai mặt phẳng (A’BC) và (ABC) bằng
thì góc giữa hai mặt phẳng (A’BC) và (ABC) bằng
A. 30o B. 60o C. 45o D. 75o