Cho hàm số y = sin2 x+2 sinx, với x∈ [ - π ; π ] . Hàm số này có mấy điểm cực trị
A. Bốn.
B. Một.
C. Ba.
D. Hai.
Kí hiệu a,b lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số f(x)=sin2 x+2 sinx trên đoạn [0;3π/2]. Giá trị a+b bằng
A. 3 3 - 2 4
B. 3 3 + 2 2
C. 3 3 - 2 2
D. 3 3 - 4 2
Biết F(x) là một nguyên hàm của hàm số f(x)=sin2 x+cosx. Giá trị F(π/2)-F(0) bằng
A. 2.
B. 1
C. -1
D. 4.
Cho hàm số f(x)=3 sinx+2. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số y = f 3 ( x ) - 3 mf 2 ( x ) + 3 ( m 2 - 4 ) f ( x ) - m nghịch biến trên khoảng (0;π/2). Số tập con của S bằng
A. 1
B. 2.
C. 4.
D. 16.
Tổng các nghiệm của phương trình 2 sin2 x+2 cosx-6 sinx-3=0 trên khoảng (0;2π) bằng
A. 3π.
B. 5π/2.
C. 17π/6.
D. 10π/3
Cho hàm số y=x+sin2 x+2017. Tìm tất cả các điểm cực tiểu của hàm số
A. x = - π / 3 + k π , k ∈ Z
B. x = - π / 3 + k 2 π , k ∈ Z
C. x = π / 3 + k 2 π , k ∈ Z
D. x = π / 3 + k π , k ∈ Z
Chứng minh rằng: sinx+tanx>2x với mọi x ∈(0;π/2)
Xét hàm số \(f\left(x\right)=sinx+tanx-2x\left(0< x< \dfrac{\pi}{2}\right)\)
\(f'\left(x\right)=cosx+\dfrac{1}{cos^2x}-2\)
mà \(cosx>cos^2x\left(0< x< \dfrac{\pi}{2}\Rightarrow0< cosx< 1\right)\)
\(\Rightarrow f'\left(x\right)=cosx+\dfrac{1}{cos^2x}-2>cos^2x+\dfrac{1}{cos^2x}-2\)
mà \(cos^2x+\dfrac{1}{cos^2x}\ge2\sqrt[]{cos^2x.\dfrac{1}{cos^2x}}=2\left(Bđt.Cauchy\right)\)
\(\Rightarrow f'\left(x\right)>2-2=0\)
\(\Rightarrow f\left(x\right)\) đồng biến trên \(0< x< \dfrac{\pi}{2}\)
\(\Rightarrow f\left(x\right)>f\left(0\right)=0,\forall x\in\left(0;\dfrac{\pi}{2}\right)\)
\(\Rightarrow sinx+tanx-2x>0\)
\(\Rightarrow sinx+tanx>2x,\forall x\in\left(0;\dfrac{\pi}{2}\right)\)
\(\Rightarrow dpcm\)
Cho hàm số f ( x ) = x 3 - 3 x . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=|f(sinx+1)+2|. Giá trị biểu thức M + m bằng
A. 4.
B. 6.
C. 2.
D. 8.
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ bên
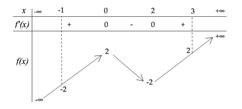
Có bao nhiêu số nguyên dương m để phương trình f(2 sinx+1)=f(m) có nghiệm thực ?
A. 2.
B. 5.
C. 4.
D. 3.
Họ nguyên hàm của hàm số f(x)=sinx+1 là
A. cosx + x + C
B. sin 2 x 2 + x + C
C. -cosx + x + C
D. cosx + C